Question 15.6: A Magnetic Circuit with Reluctances in Series and Parallel T...
A Magnetic Circuit with Reluctances in Series and Parallel
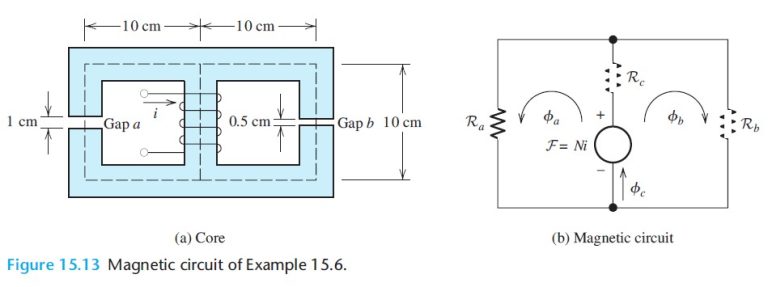
The iron core shown in Figure 15.13(a) has a cross section of 2 cm by 2 cm and a relative permeability of 1000. The coil has 500 turns and carries a current of i = 2A. Find the flux density in each air gap.
Learn more on how we answer questions.
The magnetic circuit is depicted in Figure 15.13(b). First, we compute the reluctances of the three paths. For the center path, we have
R_c=\frac{l_c}{\mu_r \mu_0 A_{\mathrm{core}}}=\frac{10 \times 10^{-2}}{1000 \times 4\pi \times 10^{-7}\times 4 \times 10^{-4}}=1.989\times 10^5\mathrm{~A\cdot turns /Wb}
For the left-hand path, the total reluctance is the sum of the reluctance of the iron core plus the reluctance of gap a. We take fringing into account by adding the gap length to its width and depth in computing area of the gap. Thus, the area of gap a is Aa = 3 cm × 3 cm = 9 × 10-4 m2. Then, the total reluctance of the left-hand path is
R_a=R_{\mathrm{gap}}+R_{\mathrm{core}}=\frac{l_{\mathrm{gap}}}{\mu_0 A_a}+\frac{l_{\mathrm{core}}}{\mu_r \mu_0A_{\mathrm{core}}} \\ =\frac{1\times 10^{-2}}{4\pi \times 10^{-7} \times 9 \times 10^{-4}}+\frac{29\times 10^{-2}}{1000 \times 4\pi \times 10^{-7} \times 4 \times 10^{-4}} \\ = 8.842 \times 10^6 +5.769\times 10^5 = 9.420 \times 10^6 \mathrm{~A\cdot turns/Wb}
Similarly, the reluctance of the right-hand path is
R_b =R_{\mathrm{gap}}+R_{\mathrm{core}}\frac{l_{\mathrm{gap}}}{\mu_0A_b}+\frac{l_{\mathrm{core}}}{\mu_r \mu_0 A_{\mathrm{core}}}
=\frac{0.5\times 10^{-2}}{4\pi \times 10^{-7} \times 6.25\times 10^{-4}}+\frac{29.5 \times 10^{-2}}{1000 \times 4\pi \times 10^{-7}\times 4 \times 10^{-4}}
=6.366 \times 10^6+5.869 \times 10^5= 6.953 \times 10^6 \mathrm{~A\cdot turns/Wb}
Next, we can combine the reluctances Ra and Rb in parallel. Then, the total reluctance is the sum of Rc and this parallel combination:
R_{\mathrm{total}}=R_c+\frac{1}{1\R_a+1/R_b}=1.989\times 10^5+\frac{1}{1/(9.420\times 10^6)+1/(6.953\times 10^{6})}
=4.199\times 10^6 \mathrm{~A\cdot turns/Wb}
Now, the flux in the center leg of the coil can be found by dividing the magnetomotive force by the total reluctance:
\phi_c=\frac{Ni}{R_{\mathrm{total}}}=\frac{500\times 2}{4.199 \times 10^6}=238.1~\mu\mathrm{Wb}
Fluxes are analogous to currents. Thus, we use the current-division principle to determine the flux in the left-hand and right-hand paths, resulting in
\phi_a=\phi_c\frac{R_b}{R_a+R_b}=238.1\times 10^{-6}\times \frac{6.953\times 10^6}{6.953\times 10^6+9.420\times 10^6}=101.1~\mu\mathrm{Wb}
Similarly, for gap b we have
\phi_b=\phi_c\frac{R_a}{R_a+R_b}=238.1\times 10^{-6}\frac{9.420\times 10^6}{6.953\times 10^6+9.420\times 10^6}=137.0~\mu\mathrm{Wb}
As a check on these calculations, we note that ɸc = ɸa + ɸb.
Now, we find the flux densities in the gaps by dividing the fluxes by the areas:
B_a=\frac{\phi_a}{A_a}=\frac{101.1~\mu\mathrm{Wb}}{9\times 10^{-4}\mathrm{~m^2}}=0.1123\mathrm{~T}
B_b=\frac{\phi_b}{A_b}=\frac{137.0~\mu\mathrm{Wb}}{6.25\times 10^{-4}\mathrm{~m^2}}=0.2192\mathrm{~T}