Question 9.CA.14: Determine the reaction at the supports for the prismatic bea......
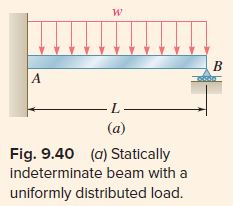
Determine the reaction at the supports for the prismatic beam and loading shown (Fig. 9.40a).
Learn more on how do we answer questions.
Consider the couple exerted at the fixed end A as redundant and replace the fixed end by a pin-and-bracket support. Couple M _A is now considered to be an unknown load (Fig. 9.40b) and will be determined from the condition that the tangent to the beam at A must be horizontal. Thus, this tangent must pass through the support B, and the tangential deviation t_{B / A} of B with respect to A must be zero. The solution is carried out by computing separately the tangential deviation \left(t_{B / A}\right)_w caused by the uniformly distributed load w (Fig. 9.40c) and the tangential deviation \left(t_{B / A}\right)_M produced by the unknown couple M _A (Fig. 9.40d).
Using the free-body diagram of the beam under the known distributed load w (Fig. 9.40e), determine the corresponding reactions at the supports A and B.
\left( R _A\right)_1=\left( R _B\right)_1=\frac{1}{2} w L \uparrow (1)
Now draw the corresponding shear and M/EI diagrams (Fig. 9.40e). Observing that M/EI is represented by an arc of parabola and recalling the formula A=\frac{2}{3} b h for the area under a parabola, the first moment of this area about a vertical axis through B is
\left(t_{B / A}\right)_w=A_1\left(\frac{L}{2}\right)=\left(\frac{2}{3} L \frac{w L^2}{8 E I}\right)\left(\frac{L}{2}\right)=\frac{w L^4}{24 E I} (2)
Using the free-body diagram of the beam when it is subjected to the unknown couple M _A (Fig. 9.40f), the corresponding reactions at A and B are
\left( R _A\right)_2=\frac{M_A}{L} \uparrow \quad\left( R _B\right)_2=\frac{M_A}{L} \downarrow (3)
Drawing the corresponding M/EI diagram (Fig. 9.40f), the second moment-area theorem is applied to obtain
\left(t_{B / A}\right)_M=A_2\left(\frac{2 L}{3}\right)=\left(-\frac{1}{2} L \frac{M_A}{E I}\right)\left(\frac{2 L}{3}\right)=-\frac{M_A L^2}{3 E I} (4)
Combining the results obtained in Eqs. (2) and (4) and expressing that the resulting tangential deviation t_{B / A} must be zero (Fig. 9.40b–d),
\begin{gathered} t_{B / A}=\left(t_{B / A}\right)_w+\left(t_{B / A}\right)_M=0 \\ \frac{w L^4}{24 E I}-\frac{M_A L^2}{3 E I}=0 \end{gathered}
and solving for M_A ,
M_A=+\frac{1}{8} w L^2 \quad M _A=\frac{1}{8} w L^2 ⤻
Substituting for M_A into Eq. (3), and recalling Eq. (1), the values of R_A and R_B are
\begin{aligned} & R_A=\left(R_A\right)_1+\left(R_A\right)_2=\frac{1}{2} w L+\frac{1}{8} w L=\frac{5}{8} w L \\ & R_B=\left(R_B\right)_1+\left(R_B\right)_2=\frac{1}{2} w L-\frac{1}{8} w L=\frac{3}{8} w L \end{aligned}

