Question 11.SP.15: Knowing that at the instant shown cylinder/ramp A has a velo...
Knowing that at the instant shown cylinder/ramp A has a velocity of 8 in./s directed down, determine the velocity of block B.
STRATEGY: You have objects connected by cables, so this is a dependent-motion problem. You should define coordinates for each bloc-kobject and write a constraint equation for the cable. You will also need to use relative motion, since B slides on A.

Learn more on how we answer questions.
MODELING and ANALYSIS: Define position vectors, as shown in Fig. 1. Constraint Equations. Assuming the cable is inextensible, you can write the length in terms of the coordinates and then differentiate.
The constraint equation for the cable is
x_A+2 x_{R A}=\text { constant }
Differentiating this gives
v_A=-2 v_{B A} (1)
Substituting for v_A gives v_{B / A}=-4 \mathrm{in} . / \mathrm{s} up the incline.
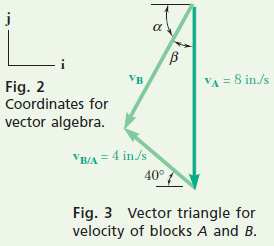
Dependent Motion: You know that the direction of v_{B/A} is directed up the incline. Therefore, the relative motion equation relating the velocities of blocks A and B is v_B = v_A + v_{B/A}. You could either draw a vector triangle or use vector algebra. Let’s use vector algebra. Using the coordinate system shown in Fig. 2 and substituting in the magnitudes gives
\left(v_B\right)_x \mathbf{i}+\left(v_B\right)_y \mathbf{j}=(-8 \text { in } / \mathrm{s}) \mathbf{j}+(-4 \text { in./s }) \sin 50^{\circ} \mathbf{i}+(4 \text { in./s }) \cos 50^{\circ} \mathbf{j}
Equating components gives
\begin{array}{ll}\mathrm{i}:\left(v_B\right)_x=-(4 \mathrm{in} . / \mathrm{s}) \sin 50^{\circ} & \rightarrow v_{B_x}=-3.064 \mathrm{in} . / \mathrm{s} \\\mathrm{j}:\left(v_B\right)_y=(-8 \mathrm{in} / \mathrm{s})+(4 \mathrm{in} / \mathrm{s}) \cos 50^{\circ} & \rightarrow v_{B_y}=-5.429 \mathrm{in} . / \mathrm{s}\end{array}
Finding the magnitude and direction gives
\mathbf{v}_B=6.23 \mathrm{in} / \mathrm{s} 60.6^{\circ}
REFLECT and THINK: Rather than using vector algebra, you could have also drawn a vector triangle, as shown in Fig. 3. To use this vector triangle, you need to use the law of cosines and the law of sines. Looking at the mechanism, block B should move up the incline if block A moves downward; our mathematical result is consistent with this. It is also interesting to note that, even though B moves up the incline relative to A, block B is actually moving down and to the left, as shown in the calculation here. This occurs because block A is also moving down.