Question 3.4: Reading Coordinates A pool cue lies on a pool table. The two......
Reading Coordinates
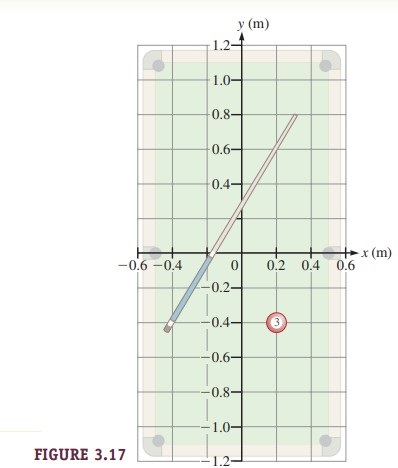
A pool cue lies on a pool table. The two-dimensional coordinate system shown in Figure 3.17 has been chosen with the origin at the center of the table.
A. What are the coordinates of the two ends of the cue?
B. How long is the cue?
C. Figure 3.19 shows a different coordinate system imposed on the same pool table we have been working with. Which of the answers above change? Which remain the same? Use this new coordinate system to find the positions of the ends of the cue as well as its length.

Learn more on how do we answer questions.
A.
INTERPRET and ANTICIPATE
In this coordinate system, the x axis is horizontal with the positive direction pointing to the right. The y axis is vertical with the positive direction pointing upward. Both axes are labeled in meters. Figure 3.16 may be used to check the sign of our answer.
SOLVE
Read off the coordinates for each end of the cue to two significant figures. We estimate that the tip (narrow end) is half way between x = 0.2 and 0.4 m.
The bumper (thick end) does not lie on a grid line. So, we must estimate both its x and y coordinates.
\left(x_b, y_b\right)=(-0.45 m ,-0.45 m )CHECK and THINK
Because the tip is in quadrant \mathrm{I}, both coordinates are positive. The bumper is in quadrant \mathrm{III}, so both coordinates are negative.
B.
INTERPRET and ANTICIPATE
Draw two distances labeled \Delta x and \Delta y to form a right triangle that has the cue as its hypotenuse (Fig. 3.18). Then, use the Pythagorean theorem to find the length of the cue.
SOLVE
First, we find the lengths \Delta x and \Delta y from the coordinates of the tip and bumper found in part B. Because we plan to square \Delta x and \Delta y, it does not matter in which order we do the subtraction.
To get the length of the cue, use the Pythagorean theorem.
\begin{aligned}\ell^2 & =\Delta x^2+\Delta y^2 \\\ell & =\sqrt{\Delta x^2+\Delta y^2} \\\ell & =\sqrt{(0.75 m )^2+(1.25 m )^2} \\ \ell & =1.46 m \end{aligned}CHECK and THINK
If you are familiar with pool, you know that a cue is somewhat shorter than an adult. So, this answer seems reasonable.
C.
INTERPRET and ANTICIPATE
Any coordinate system is artificially imposed on a physical situation, meaning that the origin can be anywhere. Because the location of the origin determines the coordinates of any object in the system, the numerical coordinates of an object change as the location of the origin changes. The length of an object cannot depend on the choice of coordinate system. Therefore, the length of the cue must still be 1.46 m.
SOLVE
The new coordinates are read off the figure. In this case, all the coordinates are positive because both ends of the cue are in quadrant \mathrm{I}.
For the cue tip:
\left(x_t, y_t\right)=(0.90 m , 2.00 m )For the cue bumper:
\left(x_b, y_b\right)=(0.15 m , 0.75 m )Recalculate the length of the cue using the same procedure as in part C but using the new coordinate system.
\begin{aligned}\Delta x & =x_t-x_b \\\Delta x & =0.90-0.15 \\\Delta x & =0.75 m \\\Delta y & =y_t-y_b \\\Delta y & =2.00-0.75 \\\Delta y & =1.25 m \\\ell & =\sqrt{(0.75 m )^2+(1.25 m )^2} \\\ell & =1.46 m\end{aligned}CHECK and THINK
As expected, the coordinates depend on the choice of coordinate system, but the length of the pool cue does not depend on the coordinate system.

