Question 2.45: Find the resistance between terminal XY of the bridge circui......
Find the resistance between terminal XY of the bridge circuit shown in Fig. 2.150, by using delta–star conversion.
Step-by-Step
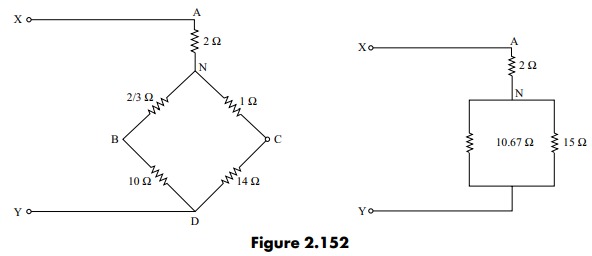
Let us change the resistances forming a delta across terminals A, B, and C into equivalent star.
\mathrm{R}_{\mathrm{A}}=\frac{\mathrm{R}_{\mathrm{AB}} \times \mathrm{R}_{\mathrm{AC}}}{\mathrm{R}_{\mathrm{AB}}+\mathrm{R}_{\mathrm{BC}}+\mathrm{R}_{\mathrm{AC}}}=\frac{4 \times 6}{4+6+2}=\frac{24}{12}=2 \Omega\\ \begin{aligned} & \mathrm{R}_{\mathrm{B}}=\frac{\mathrm{R}_{\mathrm{AB}} \times \mathrm{R}_{\mathrm{BC}}}{\mathrm{R}_{\mathrm{AB}}+\mathrm{R}_{\mathrm{BC}}+\mathrm{R}_{\mathrm{AC}}}=\frac{4 \times 2}{12}=\frac{2}{3} \Omega \\ & \mathrm{R}_{\mathrm{C}}=\frac{\mathrm{R}_{\mathrm{BC}} \times \mathrm{R}_{\mathrm{AC}}}{\mathrm{R}_{\mathrm{AB}}+\mathrm{R}_{\mathrm{BC}}+\mathrm{R}_{\mathrm{AC}}}=\frac{2 \times 6}{12}=1 \Omega \end{aligned}The equivalent star–forming resistances are
By replacing the delta resistance into equivalent star resistance, the circuit is drawn as in Fig. 2.152
The resistances of the two parallel paths between N and D are 1+14=15 \Omega \text { and } \frac{2}{3}+10=\frac{32}{3} \Omega, respectively.
Total Resistance Network Terminal X and Y
=2+\frac{15 \times 10.67}{15+10.67}=8.23 \Omega
Related Answered Questions
Question: 2.54
Verified Answer:
When the capacitor is fully charged, no current wi...
Question: 2.53
Verified Answer:
R=5.45 \times 10^6 \Omega, \quad C=1 \times...
Question: 2.52
Verified Answer:
We have,
\begin{aligned} i & =I_0\left(...
Question: 2.51
Verified Answer:
For the rise in current
i=\frac{V}{R}\left(...
Question: 2.50
Verified Answer:
Applying KCL, we can write
8=I_1+I_2[/latex...
Question: 2.49
Verified Answer:
We have shown the current directions in the variou...
Question: 2.48
Verified Answer:
Let V_A\ and\ V_B be the potential ...
Question: 2.47
Verified Answer:
Let V_A\ and\ V_B be the potentials...
Question: 2.46
Verified Answer:
We convert the delta forming resistances between t...
Question: 2.44