Question 5.7: A toroidal coil has N turns closely wound on an air core and......
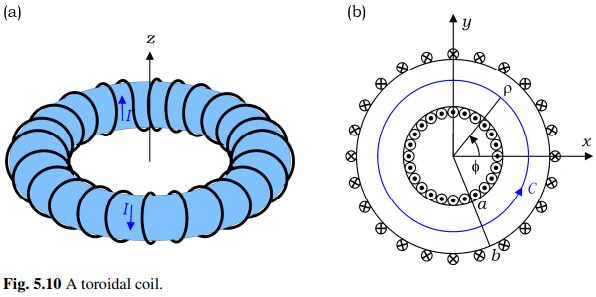
A toroidal coil has N turns closely wound on an air core and carries a steady current I as shown in Fig. 5.10. The toroid has an inner radius a and an outer radius b. Find H everywhere.
Learn more on how do we answer questions.
The closely wound toroidal coil has cylindrical symmetry (rotational symmetry about the z-axis), and thus the resulting H is independent of Φ. If the toroidal coil is rotated about the x-axis by 180º , it appears the same except for the reversed direction of the current in the coil. Note that if we reverse the current in the original coil, the direction of the resultant H should also be reversed. In view of this, we see that H cannot have the ρ– component, because the vector component H_{\rho } \pmb{a}_{ \rho } appears the same even if it is rotated about the x-axis by 180º . From these symmetry considerations so far, we arrive at a conclusion that H is of the form
\pmb{H}= H_{\phi } (\rho , z)\pmb{a}_{ \phi } + H_{z} [(\rho ,z)\pmb{a}_{z}. Assuming an ideal toroidal coil in which no current penetrates the \phi = \phi _{1} plane( \phi _{1} is constant), we see that the line integral of H around any closed path C _{1} , which lies flat on the \phi = \phi _{1} plane, is zero, i.e.,
\oint_{C_{1}}{\pmb{H} \pmb{\cdot } d \pmb{l}} = \oint_{C_{1}}{(H_{\phi } \pmb{a}_{\phi } + H_{z} \pmb{a}_{z}) \pmb{\cdot } (d \rho \pmb{a}_{\rho } + d z \pmb{a}_{z})} = \oint_{C_{1}}{H_{z} (\rho , z) dz} \\ \quad \quad \quad \quad = 0 (5-25)
Here, we use d \pmb{l} = d \rho \pmb{a}_{\rho } + dz \pmb{a}_{z} in the \phi =\phi _{1} plane. Suppose C_{1} is a rectangle with the left side at \rho =\rho _{1} and the right side at \rho =\rho _{2}, being parallel to the z-axis in the \phi =\phi _{1} plane. Since Eq. (5-25) should be satisfied regardless of the height of C_{1}, we obtain the relation H_{z} (\rho_{1} , z) = H_{z} (\rho_{2} , z) from Eq. (5-25), implying that H_{z} is constant everywhere. The finite extent of the toroidal coil, however, assures that H = 0 at infinity, meaning that H_{z} = 0 everywhere. From the discussions so far, we conclude that H of the toroidal coil is of the form \pmb{H} = H_{\phi} (\rho, z) \pmb{a}_{\phi}.
Inside the toroidal coil (a < ρ < b), taking a circle of radius ρ as an Amperian path C, from Ampere’s circuital law we obtain
\oint_{C}{\pmb{H} \pmb{\cdot } d \pmb{l}} = \oint_{C}{H_{\phi } \pmb{a}_{\phi } \pmb{\cdot } \rho d \phi \pmb{a}_{\phi } } =\rho H_{\phi } \int_{0}^{2\pi }{d \phi }= 2 \pi \rho H_{\phi }Since C encloses the total current of NI, Ampere’s circuital law gives
H_{\phi } = \frac{NI}{2 \pi \rho }Inside the toroidal coil, we have
\pmb{H} = H_{\phi } \pmb{a}_{\phi } = \frac{NI}{2 \pi \rho }\pmb{a}_{\phi } (inside) (5-26a)
Outside the toroidal coil, no net current is enclosed by C. Thus,
H = 0 (outside) (5-26b)
We notice that the final magnetic field intensity given in Eq. (5-26a) is of the form \pmb{H} = H_{\phi } (\rho ) \pmb{a}_{\phi }; it is not against our expectation of \pmb{H} = H_{\phi } (\rho, z ) \pmb{a}_{\phi }.