Question 18.1: Find the equation of, and sketch, the streamline that passes......
Find the equation of, and sketch, the streamline that passes through (1, −2) for the velocity field given by \mathbf{V}=x y \hat{\mathbf{i}}-2 y^2 \hat{\mathbf{j}} \mathrm{m} / \mathrm{s} .
Given: Velocity vector V.
Find: Streamline through (x = 1, y = −2).
Assume: No assumptions are necessary.
By definition, a streamline is everywhere tangent to the velocity field. So, the streamline through (1, −2) is tangent to the velocity V at this point. We state this relationship mathematically as
\begin{aligned} \text { slope }\left.\frac{\mathrm{d} y}{\mathrm{~d} x}\right|_{\text {streamline }} & =\frac{v}{u} \\ \frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{-2 y^2}{x y} & =\frac{-2 y}{x} . \end{aligned}Separating variables:
\frac{\mathrm{d} y}{-2 y}=\frac{\mathrm{d} x}{x} .
Integrating both sides:
\begin{aligned} \int \frac{\mathrm{d} y}{-2 y} & =\int \frac{\mathrm{d} x}{x}, \\ -\frac{1}{2} \ln y & =\ln x+C_1. \end{aligned}We have absorbed the constants of integration from both sides into this new constant C_1. Or
\ln x+\frac{1}{2} \ln y=C_2 .This new C_2 is simply −C_1 from the previous expression. To get rid of the natural logs and find a graphable function y(x), we take the exponent of the entire expression:
x \sqrt{y}=C_3, or
x^2 y=C .
This C may no longer bear much resemblance to our initial constant C_1, but the product x²y must equal some constant.
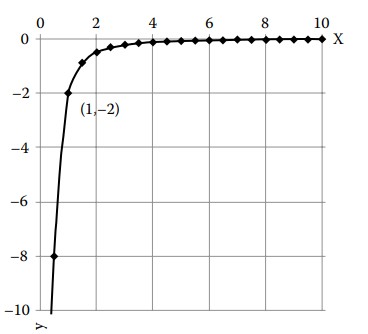
At point (1,-2), x^2 y=(1)^2(-2)=-2 , so the equation of the streamline through (1, −2) is
x^2 y=-2 .
We plot this streamline below.
