Question 5.16: Find the self-inductance per unit length of a very long sole......
Find the self-inductance per unit length of a very long solenoid, which consists of N turns per unit length tightly wound on an air core of radius a.
Learn more on how do we answer questions.
Let us explore the solenoid for symmetry:
(1) The solenoid has cylindrical symmetry (no change after rotated about the z-axis ), and translational symmetry in the z-direction (no change after displaced in the z-direction). Thus the resulting B should be of the form \pmb{B} = B_{\rho } (\rho )\pmb{a}_{\rho } + B_{\phi } (\rho )\pmb{a}_{\phi } + B_{z } (\rho )\pmb{a}_{z } at the most.
(2) The solenoid appears the same even if it is vertically flipped, or rotated about the x-axis by 180º , except for the reversed direction of the current. If the current is reversed in the original solenoid, the direction of B should be reversed at every point in space. Since the direction of B_{\rho } \pmb{a}_{\rho } remains the same when it is vertically flipped, B of the solenoid should have no ρ–component such that \pmb{B} = B_{\phi } (\rho )\pmb{a}_{\phi } + B_{z } (\rho )\pmb{a}_{z } .
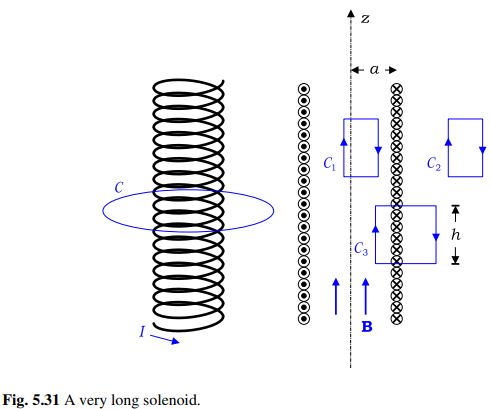
(3) The current flows only in the \pmb{a}_{\phi }-direction in an ideal solenoid, and thus no current passes through the surface of the loop C shown in Fig. 5.31. Applying Ampere’s circuital law to C, we have
\oint_{C}{ (\pmb{B} / \mu _{o}) \pmb{\cdot }d \pmb{l}} =\int_{\phi =0}^{2\pi }{( B_{\phi } (\rho )/ \mu _{o})\pmb{a}_{\phi } \pmb{\cdot }(\rho d \phi \pmb{a}_{\phi })}= 0, which results in B_{\phi }=0 . Thus, the functional form of B should be reduced to \pmb{B} = B_{z } (\rho )\pmb{a}_{z }.
Applying Ampere’s circuital law to loops C_{1} and C_{2} as shown in Fig. 5.31, by assuming \pmb{B} = B_{z } (\rho )\pmb{a}_{z }, leads to a conclusion that B is constant in the interior and exterior of the solenoid. Thus, B should be so far of the form \boxed{\pmb{B} = B_{z } \pmb{a}_{z} } everywhere.
Next, we can show that B = 0 at infinity, and thus B = 0 outside the solenoid. To start with, the solenoid is considered to be a stack of a large number of identical current loops. The magnetic field intensity of a single current loop varies with distance as 1/R³ , or 1/ (z^{2} + \rho ^{2})^{3/2} in cylindrical coordinates, as can be seen from Eq. (5-65). Thus, the total magnetic field intensity at far distances can be approximated as
\boxed{ \pmb{B}= \frac{\mu _{o} m}{4\pi R^{3}}(2\cos \theta \pmb{a}_{R} + \sin \theta \pmb{a}_{\theta })} [T] (5-65)
B\sim\int{ 1/ (z^{2} + \rho ^{2})^{-3/2} dz} \sim 1/\rho ^{2} , which becomes zero at infinity. Thus, B = 0 outside the solenoid.
Applying Ampere’s circuital law to loop C_{3} shown in Fig. 5.31, we obtain
h H_{z} = NIh
In the interior of the solenoid, we have
\pmb{H} = NI\pmb{a}_{z} (5-104a) \\ \pmb{B} =\mu _{o} NI\pmb{a}_{z} (5-104b)Total magnetic flux through the cross-section of the solenoid is
\Phi= B\pi a^{2} =\mu _{o} NI\pi a^{2}Magnetic flux linkage per unit length of the z-axis is
\Lambda = N \Phi= \mu _{o} N^{2}I\pi a^{2}Self-inductance per unit length of the solenoid is therefore
L = \frac{\Lambda}{I} = \mu _{o} N^{2}I\pi a^{2} [H/m] (5-105)