Question 2.SA.6: Using Kirchhoff’s voltage law, calculate the current circula......
Using Kirchhoff’s voltage law, calculate the current circulating in the series resistor network below:
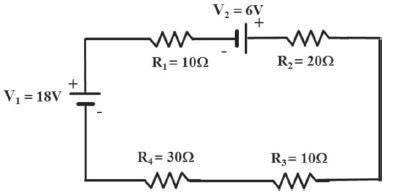
Learn more on how do we answer questions.
This problem is similar to the Example 2.2, with following exceptions:
1. The two voltage sources are driving the current in the same direction, i.e. clockwise.
2. There are four resistors in series instead of three
Using the strategy described in Example 2.2 and preparing the circuit for KVL application, the circuit would appear as follows:
Apply Ohm’s law to define the voltages, or voltage drops, across the four resis-tors. Note: since all four of the resistors are in series, we could combine them into a single REQ before applying KVL. However, in this case, we will keep resistors separate just to maintain consistency with the approach adopted in Example 2.2.
∴V_{R1}=IR_1=10(I), V_{R2}=IR_2=20(I),
V_{R3}=IR_3=10(I), and V_{R4}=IR_4=30(I)
With all voltages – voltage source, voltage load, and voltage drops across the resistors – identified and their polarities noted, apply KVL by “walking” the annotated circuit beginning at the cathode or negative electrode of the voltage source,V_{1s}. Add all voltages, with respective polarities, as you make a com-plete circle around the circuit, in the clockwise direction.
ΣV=0−18V+10(I)+−6V+20(I)+10(I)+30(I)= 0
70(I)=24 Vor,
I=\frac{24}{70}= 0.343 AAncillary exercise: Verify the derived value of current through the alternative, R_{EQ} and Ohm’s law method, as illustrated in Approach 1 of the solution for Example 2.2.
