Question 8.9: Calculate the input-referred noise, F, and SNRs for the circ......
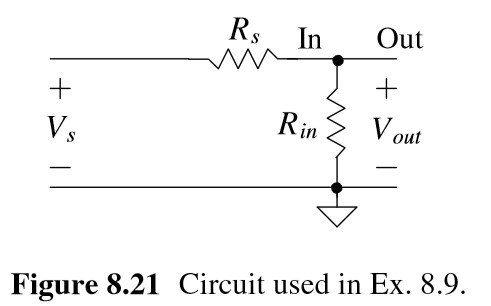
Calculate the input-referred noise, F, and SNRs for the circuit seen in Fig. 8.21.
Learn more on how do we answer questions.
Let’s begin by adding the noise voltage spectral density to the circuit, Fig. 8.22a. The output noise PSD is
Vonoise2(f)=4kTRs[Rin+RsRin]2+4kTRin[Rin+RsRs]2To determine Vonoise,RMS, we integrate this PSD over the bandwidth of interest B or
Vonoise,RMS2=∫fLfHVonoise2(f)⋅df=4kTBRs[Rin+RsRin]2+4kTBRin[Rin+RsRs]2
Noting our gain A (= Vout/Vin not Vout/Vs) is one, we can use the model shown in Fig. 8.22b. To determine the input-referred noise sources, we can use Eq. (8.32) and the results in Ex. 8.7. To determine Vinoise,RMS, we short the input to ground (Rs=0 in Fig. 8.21 and the equation above), Fig. 8.22c, and equate the circuit output to Vonoise,RMS. This gives
Vonoise,RMS2=4kTRsB⋅(Rs+RinARin)2+Iinoise,RMS2⋅(Rs+RinARsRin)2+Vinoise,RMS2⋅(Rs+RinARin)2 (8.32)
Vonoise,RMS,Rs=0=Vinoise,RMS=0
To determine Iinoise,RMS, we open the input (Rs=∞), Fig. 8.22d, and equate the Rs circuit’s output to Vonoise,RMS (from the equation above). This gives
Rin2⋅Iinoise,RMS2=Vonoise,RMS,Rs=∞2=4kTBRin→Iinoise,RMS=Rin4kTB
The input SNR is given in Eq. (8.29). The output SNR, Fig. 8.22e, is
SNRin=4kTRsB⋅[Rin+RsRin]2Vs,RMS2⋅[Rin+RsRin]2=4kTRsBVs,RMS2 (8.29)
SNRout=Vonoise,RMS2Vs,RMS2⋅[Rs+RinRin]2=4kTB⋅Rs(1+Rs/Rin)Vs,RMS2 (8.40)
The noise factor is then
F=1+RinRs (8.41)
To minimize the NF, we can decrease Rs or increase Rin. Decreasing Rs causes SNRin and SNRout to increase, as seen in Eqs. (8.29) and (8.40). At the same time, increasing Rin causes SNRout to move towards SNRin, Eq. (8.40), resulting in F moving towards 1.
