Question 8.8: A straight uniform column of length l and bending stiffness ......
A straight uniform column of length l and bending stiffness EI is subjected to uniform lateral loading w/unit length. The end attachments do not restrict rotation of the column ends. The longitudinal compressive force P has eccentricity e from the centroids of the end sections and is placed so as to oppose the bending effect of the lateral loading, as shown in Fig. P.8.8. The eccentricity e can be varied and is to be adjusted to the value, which, for given values of P and w, will result in the least maximum bending moment on the column. Show that
e=\left(w/P_{\mu^{2}}\right)\tan^{2} \mu l/4where
\mu^{2}=P/E IDeduce the end moment that gives the optimum condition when P tends to zero.
Answer: w l^{2}/16.

Learn more on how do we answer questions.
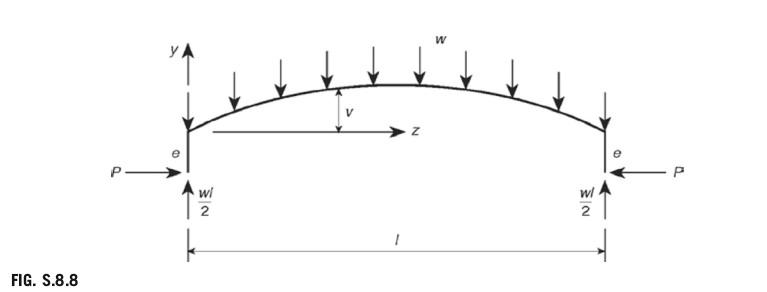
Referring to Fig. S.8.8, the bending moment at any section z is given by
M=P(e+v)-{\frac{w l}{2}}z+w{\frac{z^{2}}{2}}or
M=P(e+v)+{\frac{w}{2}}{\bigl(}z^{2}-l z{\bigr)} (i)
Substituting for M in the equation before Eq. (8.1),
E I{\cfrac{\mathrm{d}^{2}\nu}{\mathrm{d}z^{2}}}=-P_{\mathrm{CR}}\nu (8.1)
E I{\frac{\mathrm{d}^{2}v}{\mathrm{d}z^{2}}}+P v=-P e-{\frac{w}{2}}(z^{2}-l z)
or
\frac{\mathrm{d}^{2}v}{\mathrm{d}z^{2}}+\mu^{2}v=-\mu^{2}e-\frac{w\mu^{2}}{2P}(z^{2}-l z) (ii)
The solution of Eq. (ii) is
v=A\cos\mu z+B\sin\mu z-e+{\frac{w}{2P}}{\big(}l z-z^{2}{\big)}+{\frac{w}{\mu^{2}P}} (iii)
When z = 0, υ =0, hence A = e – w/μ²P. When z=l/2, dυ/dz = 0, which gives
B=A\tan{\frac{\mu l}{2}}=\left(e-{\frac{w}{\mu^{2}{ P}}}\right)\tan{\frac{\mu l}{2}}Eq. (iii) then becomes
\ v=\left(e-{\frac{w}{\mu^{2}{P}}}\right)\left[{\frac{\cos\mu(z-l/2)}{\cos\mu l/2}}-1\right]+{\frac{w}{2P}}(l z-z^{2}) (iv)
The maximum bending moment will occur at mid-span where z=l/2 and υ = υ_{max}.
From Eq. (iv),
v_{\mathrm{max}}=\left(e-{\frac{E I w}{P^{2}}}\right)\left(\sec{\frac{\mu l}{2}}-1\right)+{\frac{w l^{2}}{8P}}and from Eq. (i),
M(\operatorname{max})=P e+P v_{\operatorname*{max}}-{\frac{w l^{2}}{8}}whence,
M(\operatorname{max})=\left(P e-{\frac{w}{\mu^{2}}}\right)\sec{\frac{\mu l}{2}}+{\frac{w}{\mu^{2}}}For the maximum bending moment to be as small as possible, the bending moment at the ends of the column must be numerically equal to the bending moment at mid-span. Thus,
P e+\left(P e-\frac{w}{\mu^{2}}\right)\sec\frac{\mu l}{2}+\frac{w}{\mu^{2}}=0or
P e\biggl(1+\sec{\frac{\mu l}{2}}\biggr)={\frac{w}{\mu^{2}}}\biggl(\sec{\frac{\mu l}{2}}-1\biggr)Then
e={\frac{w}{P\mu^{2}}}{\left({\frac{1-\cos\mu l/2}{1+\cos\mu l/2}}\right)}i.e.,
e=\left({\frac{w}{P\mu^{2}}}\right)\tan^{2}{\frac{\mu l}{4}} (vi)
From Eq. (vi), the end moment is
P e={\frac{w}{\mu^{2}}}\mathrm{tan}^{2}{\frac{\mu l}{4}}={\frac{w l^{2}}{16}}\left({\frac{\tan\mu l/4}{\mu l/4}}\right)\left({\frac{\tan\mu l/4}{\mu l/4}}\right)When P\rightarrow0,\tan\mu l/4\rightarrow\mu l/4 and the end moment becomes wl²/16.