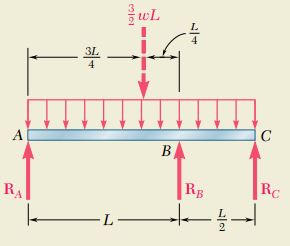
Question 11.SP.7: For the uniform beam and loading shown, determine the reacti...

Castigliano’s Theorem. The beam is indeterminate to the first degree and we choose the reaction $\mathbf{R}_{A}$ as redundant. Using Castigliano’s theorem, we determine the deflection at $A$ due to the combined action of $\mathbf{R}_{A}$ and the distributed load. Since $E I$ is constant, we write

$y_{A}=\int \frac{M}{E I}\left(\frac{\partial M}{\partial R_{A}}\right) d x=\frac{1}{E I} \int M \frac{\partial M}{\partial R_{A}} d x$     (1)

The integration will be performed separately for portions $A B$ and $B C$ of the beam. Finally, $\mathbf{R}_{A}$ is obtained by setting $y_{A}$ equal to zero.

Free Body: Entire Beam. We express the reactions at $B$ and $C$ in terms of $R_{A}$ and the distributed load

$R_{B}=\frac{9}{4} w L-3 R_{A} \quad R_{C}=2 R_{A}-\frac{3}{4} w L$    (2)

Portion AB of Beam. Using the free-body diagram shown, we find

$M_{1}=R_{A} x-\frac{w x^{2}}{2} \quad \frac{\partial M_{1}}{\partial R_{A}}=x$

Substituting into Eq. (1) and integrating from $A$ to $B$, we have

$\frac{1}{E I} \int M_{1} \frac{\partial M}{\partial R_{A}} d x=\frac{1}{E I} \int_{0}^{L}\left(R_{A} x^{2}-\frac{w x^{3}}{2}\right) d x=\frac{1}{E I}\left(\frac{R_{A} L^{3}}{3}-\frac{w L^{4}}{8}\right)$    (3)

Portion BC of Beam. We have

$M_{2}=\left(2 R_{A}-\frac{3}{4} w L\right) v-\frac{w v^{2}}{2} \quad \frac{\partial M_{2}}{\partial R_{A}}=2 v$

Substituting into Eq. (1) and integrating from $C$, where $v=0$, to $B$, where $v=\frac{1}{2} L$, we have

Reaction at $\boldsymbol{A}$. Adding the expressions obtained in (3) and (4), we determine $y_{A}$ and set it equal to zero

$y_{A}=\frac{1}{E I}\left(\frac{R_{A} L^{3}}{3}-\frac{w L^{4}}{8}\right)+\frac{1}{E I}\left(\frac{R_{A} L^{3}}{6}-\frac{5 w L^{4}}{64}\right)=0$

Solving for $R_{A}, \quad R_{A}=\frac{13}{32} w L \quad R_{A}=\frac{13}{32} w L \uparrow$

Reactions at $\boldsymbol{B}$ and $\boldsymbol{C}$. Substituting for $R_{A}$ into Eqs. (2), we obtain

$R_{B}=\frac{33}{32} w L \uparrow \quad R_{C}=\frac{w L}{16} \uparrow$