Question A.06: Determine the moment of inertia Ix of the area shown with re...
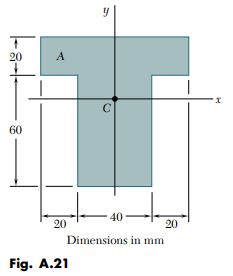
Determine the moment of inertia \bar{I}_{x} of the area shown with respect to the centroidal x axis (Fig. A.21).
Learn more on how we answer questions.
Location of Centroid. The centroid C of the area must first be located. However, this has already been done in Example A.02 for the given area. We recall from that example that C is located 46 \mathrm{~mm} above the lower edge of the area A.
Computation of Moment of Inertia. We divide the area A into the two rectangular areas A_{1} and A_{2} (Fig. A.22), and compute the moment of inertia of each area with respect to the x axis.
Rectangular Area A_{1}. To obtain the moment of inertia \left(I_{x}\right)_{1} of A_{1} with respect to the x axis, we first compute the moment of inertia of A_{1} with respect to its own centroidal axis x^{\prime}. Recalling the formula derived in part a of Example A.04 for the centroidal moment of inertia of a rectangular area, we have
\left(\bar{I}_{x^{\prime}}\right)_{1}=\frac{1}{12} b h^{3}=\frac{1}{12}(80 \mathrm{~mm})(20 \mathrm{~mm})^{3}=53.3 \times 10^{3} \mathrm{~mm}^{4}
Using the parallel-axis theorem, we transfer the moment of inertia of A_{1} from its centroidal axis x^{\prime} to the parallel axis x :
\begin{aligned} \left(I_{x}\right)_{1}=\left(\bar{I}_{x^{\prime}}\right)_{1}+A_{1} d_{1}^{2}= & 53.3 \times 10^{3}+(80 \times 20)(24)^{2} \\ = 975 × 10³ \text{ mm}^4 \end{aligned}
Rectangular Area A_{2}. Computing the moment of inertia of A_{2} with respect to its centroidal axis x^{\prime \prime}, and using the parallel-axis theorem to transfer it to the x axis, we have
\begin{aligned} \left(\bar{I}_{x^{\prime \prime}}\right)_{2} & =\frac{1}{12} b h^{3}=\frac{1}{12}(40)(60)^{3}=720 \times 10^{3} \mathrm{~mm}^{4} \\ \left(I_{x}\right)_{2} & =\left(\bar{X}_{x^{\prime \prime}}\right)_{2}+A_{2} d_{2}^{2}=720 \times 10^{3}+(40 \times 60)(16)^{2} \\ & =1334 \times 10^{3} \mathrm{~mm}^{4} \end{aligned}
Entire Area A. Adding the values computed for the moments of inertia of A_{1} and A_{2} with respect to the x axis, we obtain the moment of inertia \bar{I}_{x} of the entire area:
\begin{aligned} & \bar{I}_{x}=\left(I_{x}\right)_{1}+\left(I_{x}\right)_{2}=975 \times 10^{3}+1334 \times 10^{3} \\ & \bar{I}_{x}=2.31 \times 10^{6} \mathrm{~mm}^{4} \end{aligned}
