Question 17–4: A 10-hp split-phase motor running at 1750 rev/min is used to...

The peripheral speed V of the belt is

Table 17–11: L_{p}=L+L_{c}=112+1.8=113.8 \text { in }

Eq. (17–16b): \begin{aligned}C=& 0.25\left\{\left[113.8-\frac{\pi}{2}(11+7.4)\right]\right.\\&\left.+\sqrt{\left[113.8-\frac{\pi}{2}(11+7.4)\right]^{2}-2(11-7.4)^{2}}\right\}\end{aligned}

= 42.4 in

C=0.25\left\{\left[L_{p}-\frac{\pi}{2}(D+d)\right]+\sqrt{\left[L_{p}-\frac{\pi}{2}(D+d)\right]^{2}-2(D-d)^{2}}\right\}    (17–16b)

Eq. (17–1):\begin{array}{c}\phi=\theta_{d}=\pi-2 \sin ^{-1}(11-7.4) /[2(42.4)]=3.057 rad \\\exp[0.5123(3.057)]=4.788\end{array}

\theta_{D}=\pi+2 \sin ^{-1} \frac{D-d}{2 C}        (17–1)

Interpolating in Table 17–12 for V = 3390 ft/min givesH_{ tab }=4.693 hp. The wrap angle in degrees is 3.057(180) / \pi=175^{\circ} .. From Table 17–13, K1 5 0.99. From Table 17–14, K_{2}=1.05 . Thus, from Eq. (17–17),

H_{a}=K_{1} K_{2} H_{ tab }        (17–17)

Eq. (17–19):  H_{d}=H_{ nom } K_{s} n_{d}=10(1.2+0.1)(1)=13 hp

H_{d}=H_{ nom } K_{s} n_{d}    (17–19)

Eq. (17–20): N\geq H_{d}/H_{a}=13/4.878=2.67\rightarrow 3

N_{b} \geq \frac{H_{d}}{H_{a}} \quad N_{b}=1,2,3, \ldots    (17–20)

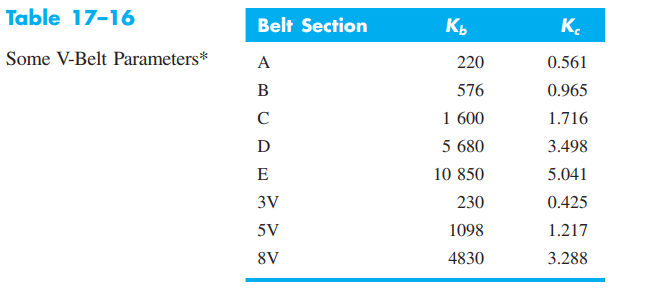
From Table 17–16, K_{c}=0.965. Thus, from Eq. (17–21),

F_{c}=K_{c}\left(\frac{V}{1000}\right)^{2}    (17–21)

Eq. (17–22): \Delta F=\frac{63025(13) / 3}{1750(7.4 / 2)}=42.2 lbf

\Delta F=\frac{63025 H_{d} / N_{b}}{n(d / 2)}    (17–22)

Eq. (17–23): F_{1}=11.1+\frac{42.2(4.788)}{4.788-1}=64.4 lbf

F_{1}=F_{c}+\frac{\Delta F \exp (f \phi)}{\exp (f \phi)-1}    (17–23)

Eq. (17–24):  F_{2}=F_{1}-\Delta F=64.4-42.2=22.2 lbf

F_{2}=F_{1}-\Delta F     (17–24)

Eq. (17–25): F_{i}=\frac{64.4+22.2}{2}-11.1=32.2 lbf

F_{i}=\frac{F_{1}+F_{2}}{2}-F_{c}      (17–25)

Eq. (17–26): n_{f s}=\frac{H_{a} N_{b}}{H_{ nom } K_{s}}=\frac{4.878(3)}{10(1.3)}=1.13

n_{f s}=\frac{H_{a} N_{b}}{H_{ nom } K_{s}}      (17–26)

Life: From Table 17–16, K_{b}=576 .

From Table 17–17, K = 1193 and b = 10.926.

N_{P}=\left[\left(\frac{K}{T_{1}}\right)^{-b}+\left(\frac{K}{T_{2}}\right)^{-b}\right]^{-1}    (17–27)

Since N_{P} is out of the validity range of Eq. (17–27), life is reported as greater than 10^{9} passes. Then

Eq. (17–28): t>\frac{10^{9}(113.8)}{720(3390)}=46600 h

t=\frac{N_{P} L_{p}}{720 V }    (17–28)