Question 3.12: Two forces of the same magnitude P act on a cube of side a a......
Two forces of the same magnitude P act on a cube of side a as shown. Replace the two forces by an equivalent wrench, and determine ( a ) the magnitude and direction of the resultant force R , ( b ) the pitch of the wrench, ( c ) the point where the axis of the wrench intersects the yz plane.

Learn more on how we answer questions.
Equivalent Force-Couple System at O . We first determine the equivalent force-couple system at the origin O . We observe that the position vectors of the points of application E and D of the two given forces are {r}_{E}\,=a \mathrm{i }\ + a \mathrm {j} \,\operatorname{and}\, {r}_{D}~=~a \mathrm{j~}+~a\mathrm{k}. The resultant R of the two forces and their moment resultant {M}_{O}^{R} about O are
\mathrm{R}=\mathrm{F}_{1}+\mathrm{F}_{2}=P\mathrm{i}+P\mathrm{j}=P(\mathrm{i}+\mathrm{j}) (1)
{M}_{O}^{R}~=~ {r}_{E}~ \times ~{F}_{1} ~+~ {r}_{D}~\times~{F}_{2}~=(a\mathrm{i}~+~a\mathrm{{j}}~)\times~ P\mathrm{i}~+~(a\mathrm{j}~+~a\mathrm{k})~\times ~P \mathrm{j} \\ \\ ~~~~~=\,-P a\mathrm{k}-P a\mathrm{i}=\,-P a(\mathrm{i}\,+\,\mathrm{k}) (2)
a. Resultant Force R. It follows from Eq. (1) and the adjoining sketch that the resultant force R has the magnitude R=P\,1\,{\bar 2}, lies in the xy plane, and forms angles of 45° with the x and y axes. Thus
R\,=\,P\,1\,{\overline{{2}}}\qquad \mathrm u_{x}\,=\, \mathrm u_{y}\,=\,45^{\circ}\qquad \mathrm u_{z}\,=\,90^{\circ}b. Pitch of Wrench. Recalling formula (3.62)
p=\frac{M_{1}}{R}=\frac{{R}\cdot{M}_{O}^{R}}{R^{2}} (3.62)
of Sec. 3.21 and Eqs. (1) and (2) above, we write
p={\frac{ {R}\cdot {M}_{O}^{R}}{R^{2}}}={\frac{P(\mathrm{i}+\mathrm{j})\cdot(-P a)(\mathrm{i}+\mathrm{k})}{(P2\bar{2} )^{2}}}={\frac{-P^{2}a(1+0+0)}{2P^{2}}}\ p=-{\frac{a}{2}}c. Axis of Wrench. It follows from the above and from Eq. (3.61)
{M}_{1}=\,p{R} (3.61)
that the wrench consists of the force R found in (1) and the couple vector
{M}_{1~}=~p {R}~=~ -{\frac{a}{2}}P~(\mathrm{ {i}}~+~\mathrm{ {j}})\,=\,-{\frac{P a}{2}}~\left(\mathrm{{i}}~+~\mathrm{{j}}\right) (3)
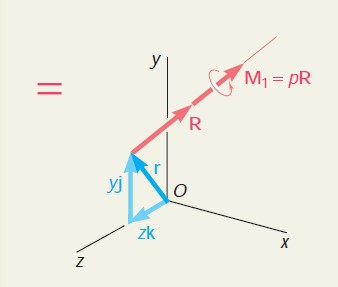
To find the point where the axis of the wrench intersects the yz plane, we express that the moment of the wrench about O is equal to the moment resultant {M}_{O}^{R} of the original system:
{M}_{1}+ {r}\times {R}= {M}_{O}^{\mathrm{R}}or, noting that r = y j + z k and substituting for R, {M}_{O}^{R} , and {M}_{1} from Eqs. (1), (2), and (3),
-{\frac{P a}{2}}(\mathrm{ {i}}+\mathrm{j})\,+\,(y\mathrm{ {j}}+\,z\mathrm{ {k}})\,\times\,P(\mathrm{ {i}}+\mathrm{ {j}})\,=\,-P a(\mathrm{ {i}}\,+\,\mathrm{ {k}}) \\ \\ -{\frac{P a}{2}}{\mathrm i}-{\frac{P a}{2}}{\mathrm{ {j}}}-P y{\mathrm{k}}+P z{\mathrm{j}}-P z{ {\mathrm{i}}}=-P a{\mathrm i}-P a{\mathrm{k}}Equating the coefficients of k , and then the coefficients of j , we find
y = a z = a/2