Question 4.8: A 5 × 8-ft sign of uniform density weighs 270 lb and is supp......
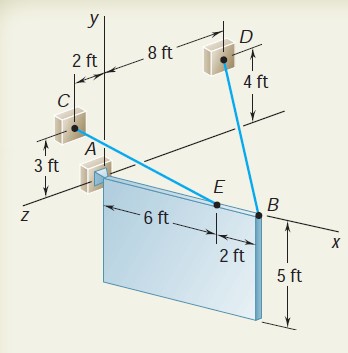
A 5 × 8-ft sign of uniform density weighs 270 lb and is supported by a ball-and-socket joint at A and by two cables. Determine the tension in each cable and the reaction at A.
Learn more on how we answer questions.
Free-Body Diagram. A free-body diagram of the sign is drawn. The forces acting on the free body are the weight W = -(270 lb)j and the reactions at A, B, and E. The reaction at A is a force of unknown direction and is represented by three unknown components. Since the directions of the forces exerted by the cables are known, these forces involve only one unknown each, namely, the magnitudes T_{B D}{\mathrm{~and~}}T_{E C}. Since there are only five unknowns, the sign is partially constrained. It can rotate freely about the x axis; it is, however, in equilibrium under the given loading, since the equation \Sigma M_{x}=0 is satisfied.
The components of the forces T_{B D}{\mathrm{~and~}}T_{E C} can be expressed in terms of the unknown magnitudes T_{B D}{\mathrm{~and~}}T_{E C} by writing
{\overrightarrow{B D}}=-(8\mathrm{~ft}){\mathrm i}+(4\mathrm{~ft}){\mathrm j}-(8\mathrm{~ft}){\mathrm k}\qquad{\mathit{B D}}=12\mathrm{~ft} \\ \\ {{\overrightarrow{{E C}} }}\,=\,-(6\,{\mathrm{ft}}){\mathrm{i}}\,+\,(3\,{\mathrm{ft}}){\mathrm{j}}\,+\,(2\,{\mathrm{ft}}){\mathrm{k}}\qquad E C\,=\,7\,{\mathrm{ft}}{T}_{B D}~=~{T}_{B D}\left(\frac{\overrightarrow{BD} }{BD} \right) ~=T_{B D}(-{\textstyle\frac{2}{3}}\mathrm{i}\,+\,{\textstyle\frac{1}{3}}\mathrm{j}\,-\,{\textstyle\frac{2}{3}}\mathrm{k}) \\ \\ {T}_{EC}~=~{T}_{EC}\left(\frac{\overrightarrow{EC} }{EC} \right) ~=T_{EC}(-{\textstyle\frac{6}{7}}\mathrm{i}\,+\,{\textstyle\frac{3}{7}}\mathrm{j}\,-\,{\textstyle\frac{2}{7}}\mathrm{k})
Equilibrium Equations. We express that the forces acting on the sign form a system equivalent to zero:
(2.667~T_{B D}+2.571~T_{E C}-1080\ \mathrm{l b}){\mathrm k}\,+\,(5.333~T_{B D}-\ 1.714~T_{E C}){\mathrm j}=0 (2)
Setting the coefficients of j and k equal to zero in Eq. (2), we obtain two scalar equations which can be solved for T_{B D}{\mathrm{~and~}}T_{E C}:
T_{B D}=101.3 ~\mathrm{lb}\qquad T_{E C}=315~{\mathrm{lb}}Setting the coefficients of i, j, and k equal to zero in Eq. (1), we obtain
three more equations, which yield the components of A. We have
A = +(338 lb)i + (101.2 lb)j – (22.5 lb)k
