Question 4.SP.6: A man raises a 10-kg joist with a length of 4 m by pulling o......

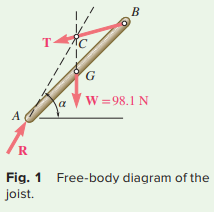
STRATEGY: The joist is acted upon by three forces: its weight W, the force T exerted by the rope, and the reaction R of the ground at A. Therefore, it is a three-force body, and you can compute the forces by using a force triangle.

MODELING: First note that

W = mg = (10 kg)(9.81 m/s²) = 98.1 N

Because the joist is a three-force body, the forces acting on it must be concurrent. The reaction R therefore must pass through the point of intersection C of the lines of action of the weight W and the tension force T, as shown in the free-body diagram (Fig. 1). You can use this fact to determine the angle α that R forms with the horizontal.

ANALYSIS: Draw the vertical line BF through B and the horizontal line CD through C (Fig. 2). Then

AF = BF = (AB) cos 45° = (4 m) cos 45° = 2.828 m

CD = EF = AE = {\frac{1}{2}}(AF) = 1.414 m

BD = (CD) cot (45° + 25°) = (1.414 m) tan 20° = 0.515 m

CE = DF = BF − BD = 2.828 m − 0.515 m = 2.313 m

From these calculations, you can determine the angle α as

\tan\alpha={\frac{C E}{A E}}={\frac{2.313\mathrm{~m}}{1.414\mathrm{~m}}}=1.636

α = 58.6° ◂

You now know the directions of all the forces acting on the joist.

Force Triangle. Draw a force triangle as shown (Fig. 3) with its interior angles computed from the known directions of the forces. You can then use the law of sines to find the unknown forces.

{\frac{T}{\sin{31.4}^{\circ}}}={\frac{R}{\sin{110^{\circ}}}}={\frac{98.1\,\mathrm{N}}{\sin{{38.6^{\circ}}}}}

T = 81.9 N ◂

R = 147.8 N ⦨ 58.6° ◂

REFLECT and THINK: In practice, three-force members occur often, so learning this method of analysis is useful in many situations.