Question 15.2: The double gear shown rolls on the stationary lower rack; th......
The double gear shown rolls on the stationary lower rack; the velocity of its center A is 1.2 m/s directed to the right. Determine (a) the angular velocity of the gear, (b) the velocities of the upper rack R and of point D of the gear.

Learn more on how we answer questions.
a. Angular Velocity of the Gear. Since the gear rolls on the lower rack, its center A moves through a distance equal to the outer circumference 2pr1 for each full revolution of the gear. Noting that 1 rev = 2p rad, and that when A moves to the right (xA > 0) the gear rotates clockwise (u < 0), we write
2pr1xA=−2puxA=−r1uDifferentiating with respect to the time t and substituting the known values
vA=1.2 m/s and r1=150 mm=0.150 m, we obtain
vA=−r1v1.2 m/s=−(0.150 m)vv=−8 rad/sV=vk=−(8 rad/s)kwhere k is a unit vector pointing out of the paper.
b. Velocities. The rolling motion is resolved into two component motions: a translation with the center A and a rotation about the center A. In the translation, all points of the gear move with the same velocity vA. In the rotation, each point P of the gear moves about A with a relative velocity vP/A=vk×rP/A , where rP/A is the position vector of P relative to A.
Velocity of Upper Rack. The velocity of the upper rack is equal to the velocity of point B; we write
vR=vB=vA+vB/A=vA+vk×rB/A= (1.2 m/s)i – (8 rad/s)k × (0.100 m)j
= (1.2 m/s)i + (0.8 m/s)i = (2 m/s)i
vR=2 m/s yVelocity of Point D
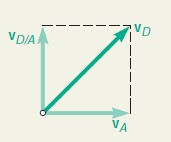
vD=vA+vD/A=vA+vk×rD/A= (1.2 m/s)i – (8 rad/s)k × (-0.150 m)i
= (1.2 m/s)i + (1.2 m/s)j
vD=1.697 m/s a 45∘