Question 15.3: In the engine system shown, the crank AB has a constant cloc......
In the engine system shown, the crank AB has a constant clockwise angular velocity of 2000 rpm. For the crank position indicated, determine (a) the angular velocity of the connecting rod BD, (b) the velocity of the piston P.

Learn more on how we answer questions.
Motion of Crank AB. The crank AB rotates about point A. Expressing \text v_{AB} in rad/s and writing v_B = r \text v_{AB}, we obtain
\text v _{A B}=\left(2000 \frac{ rev }{ min }\right)\left(\frac{1~ min }{60~ s }\right)\left(\frac{2 p ~rad }{1 ~rev }\right)=209.4~rad / s \\ \\v_B=(A B)\text v _{A B}=(3~ in .)(209.4~ rad / s )=628.3~ in . / s\\ \\ \text v _B=628.3~ { in. } / s~ c~ 50^{\circ}Motion of Connecting Rod BD. We consider this motion as a general plane motion. Using the law of sines, we compute the angle b between the connecting rod and the horizontal
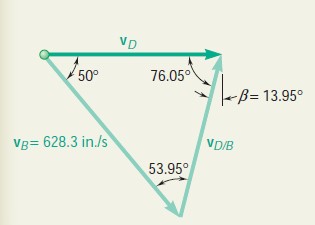
\frac{\sin ~40^{\circ}}{8 ~ {in.}}=\frac{\sin~ b}{3 ~ { in. }} \quad\quad\quad b=13.95^{\circ}The velocity \text v_D of the point D where the rod is attached to the piston must be horizontal, while the velocity of point B is equal to the velocity \text v_B obtained above. Resolving the motion of BD into a translation with B and a rotation about B, we obtain
Expressing the relation between the velocities \text v _D,\text v _B \text {, and}~\text v _{D / B} \text {, } we write
\text v _D=\text v _B+\text v _{D / B}We draw the vector diagram corresponding to this equation. Recalling that b = 13.95°, we determine the angles of the triangle and write
\frac{v_D}{\sin 53.95^{\circ}}=\frac{v_{D / B}}{\sin 50^{\circ}}=\frac{628.3~ in . / s }{\sin 76.05^{\circ}}v_{D / B}=495.9~ in. / s \quad\quad\quad \text v _{D / B}=495.9~ in. / s ~\text {a}~ 76.05^{\circ}
v_D=523.4~ in . / s =43.6~ ft / s \quad\quad\quad\text v _D=43.6~ ft / s ~\text y
\text v _P=\text v _D=43.6~ ft / s ~\text y
Since v_{D / B}=l \text v _{B D}, we have
495.9~ in . / s =(8~ in .) \text v_{B D} \quad\quad\quad \text V_{B D}=62.0 ~rad / s l