Question 6.SP.2: Determine the forces in members EF and GI of the truss shown......
Determine the forces in members EF and GI of the truss shown.
STRATEGY: You are asked to determine the forces in only two of the members in this truss, so the method of sections is more appropriate than the method of joints. You can use a free-body diagram of the entire truss to help determine the reactions, and then pass sections through the truss to isolate parts of it for calculating the desired forces.

Learn more on how we answer questions.
MODELING and ANALYSIS: You can go through the steps that follow for the determination of the support reactions, and then for the analysis of portions of the truss.
Free-Body: Entire Truss. Draw a free-body diagram of the entire truss. External forces acting on this free body consist of the applied loads and the reactions at B and J (Fig. 1). Write and solve the following equilibrium equations.
+↺ \Sigma M_B=0:
-(28 ~\mathrm{kips})(8 ~\mathrm{ft})-(28 ~\mathrm{kips})(24 ~\mathrm{ft})-(16 ~\mathrm{kips})(10 ~\mathrm{ft})+J(32 ~\mathrm{ft})=0
J=+33 \text { kips } \quad \mathbf{J}=33 \text { kips } \uparrow
\stackrel{+}{\rightarrow} \Sigma F_x=0: \quad B_x+16 \text { kips }=0
B_x=-16 \text { kips } \quad \mathbf{B}_x=16 \text { kips } \leftarrow
+↺ \Sigma M_J=0:
(28 ~\mathrm{kips})(24 ~\mathrm{ft})+(28 ~\mathrm{kips})(8 ~\mathrm{ft})-(16~ \mathrm{kips})(10 ~\mathrm{ft})-B_y(32 ~\mathrm{ft})=0
B_y=+23 \text { kips } \quad \mathbf{B}_y=23 \text { kips } \uparrow
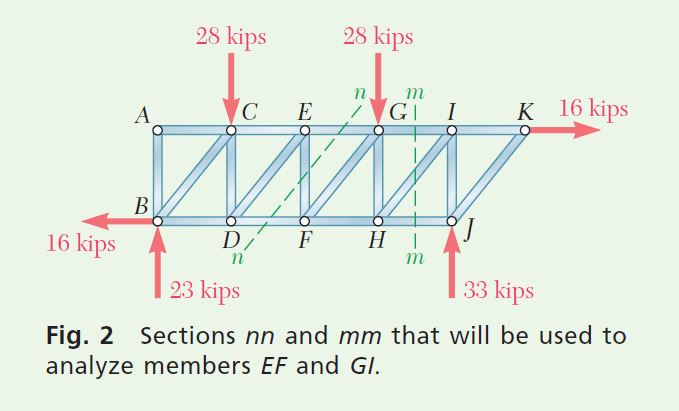
Force in Member EF. Pass section nn through the truss diagonally so that it intersects member EF and only two additional members (Fig. 2).
Remove the intersected members and choose the left-hand portion of the truss as a free body (Fig. 3). Three unknowns are involved; to eliminate the two horizontal forces, we write
+\uparrow \Sigma F_y=0: \quad+23 \text { kips }-28 \text { kips }-F_{E F}=0
F_{E F}=-5 \text { kips }
The sense of \mathbf{F}_{E F} was chosen assuming member EF to be in tension; the negative sign indicates that the member is in compression.
F_{E F}=5 \text { kips } C
Force in Member GI. Pass section mm through the truss vertically so that it intersects member GI and only two additional members (Fig. 2). Remove the intersected members and choose the right-hand portion of the truss as a free body (Fig. 4). Again, three unknown forces are involved; to eliminate the two forces passing through point H, sum the moments about that point.
+↺ \Sigma M_H=0: \quad(33 ~\mathrm{kips})(8 ~\mathrm{ft})-(16 ~\mathrm{kips})(10 ~\mathrm{ft})+F_{G I}(10 ~\mathrm{ft})=0
F_{G I}=-10.4 \text { kips } \quad F_{G I}=10.4 \text { kips } C
REFLECT and THINK: Note that a section passed through a truss does not have to be vertical or horizontal; it can be diagonal as well. Choose the orientation that cuts through no more than three members of unknown force and also gives you the simplest part of the truss for which you can write equilibrium equations and determine the unknowns.