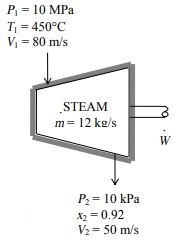
Question 6.52: Steam flows steadily through an adiabatic turbine. The inlet......
Steam flows steadily through an adiabatic turbine. The inlet conditions of the steam are 10 \mathrm{MPa}, 450^{\circ} \mathrm{C}, and 80 \mathrm{~m} / \mathrm{s}, and the exit conditions are 10 \mathrm{kPa}, 92 percent quality, and 50 \mathrm{~m} / \mathrm{s}. The mass flow rate of the steam is 12 \mathrm{~kg} / \mathrm{s}. Determine (a) the change in kinetic energy, (b) the power output, and (c) the turbine inlet area.

Learn more on how do we answer questions.
Steam expands in a turbine. The change in kinetic energy, the power output, and the turbine inlet area are to be determined.
Assumptions 1 This is a steady-flow process since there is no change with time. 2 Potential energy changes are negligible. \mathrm{3} The device is adiabatic and thus heat transfer is negligible.
Properties From the steam tables (Tables A-4 through 6)
\left.\begin{array}{l} P_{1}=10 \mathrm{MPa} \\ T_{1}=450^{\circ} \mathrm{C} \end{array}\right\} \begin{gathered} {v}_{1}=0.029782 \mathrm{~m}^{3} / \mathrm{kg} \\ h_{1}=3242.4 \mathrm{~kJ} / \mathrm{kg} \end{gathered}
and
\left.\begin{array}{l} P_{2}=10 \mathrm{kPa} \\ x_{2}=0.92 \end{array}\right\} h_{2}=h_{f}+x_{2} h_{f g}=191.81+0.92 \times 2392.1=2392.5 \mathrm{~kJ} / \mathrm{kg}
Analysis (a) The change in kinetic energy is determined from
\Delta k e=\frac{V_{2}^{2}-V_{1}^{2}}{2}=\frac{(50 \mathrm{~m} / \mathrm{s})^{2}-(80 \mathrm{~m} / \mathrm{s})^{2}}{2}\left\lgroup\frac{1 \mathrm{~kJ} / \mathrm{kg}}{1000 \mathrm{~m}^{2} / \mathrm{s}^{2}}\right\rgroup=-\mathrm{1 . 9 5} \mathrm{k J} / \mathrm{k g}
(b) There is only one inlet and one exit, and thus \dot{m}_{1}=\dot{m}_{2}=\dot{m}. We take the turbine as the system, which is a control volume since mass crosses the boundary. The energy balance for this steady-flow system can be expressed in the rate form as
\begin{aligned} & \underbrace{\dot{E}_{\text {in }}-\dot{E}_{\text {out }}}_{\begin{array}{c} \text { Rate of net energy transfer } \\ \text { by heat, work, and mass } \end{array}}=\underbrace{\Delta \dot{E}_{\text {system }}{}^{\nearrow 0 \text { (steady) }}}_{\begin{array}{c} \text { Rate of change in internal, kinetic, } \\ \text { potential, etc. energies } \end{array}}=0 \\ & \dot{E}_{\text {in }}=\dot{E}_{\text {out }} \\ & \dot{m}\left(h_{1}+V_{1}^{2} / 2\right)=\dot{W}_{\text {out }}+\dot{m}\left(h_{2}+V_{2}^{2} / 2\right) \quad(\text { since } \dot{Q} \cong \Delta \mathrm{pe} \cong 0) \\ & \dot{W}_{\text {out }}=-\dot{m}\left\lgroup h_{2}-h_{1}+\frac{V_{2}^{2}-V_{1}^{2}}{2}\right\rgroup \end{aligned}
Then the power output of the turbine is determined by substitution to be
\dot{W}_{\text {out }}=-(12 \mathrm{~kg} / \mathrm{s})(2392.5-3242.4-1.95) \mathrm{kJ} / \mathrm{kg}=\mathrm{1 0 . 2} \mathrm{~ M W}
(c) The inlet area of the turbine is determined from the mass flow rate relation,
\dot{m}=\frac{1}{v_{1}} A_{1} V_{1} \longrightarrow A_{1}=\frac{\dot{m} v_{1}}{V_{1}}=\frac{(12 \mathrm{~kg} / \mathrm{s})\left(0.029782 \mathrm{~m}^{3} / \mathrm{kg}\right)}{80 \mathrm{~m} / \mathrm{s}}=\mathrm{0 . 0 0 4 4 7} \mathrm{m}^{2}