Question 26.18: The Z-section beam shown in Fig. P.26.18 carries a bending m......
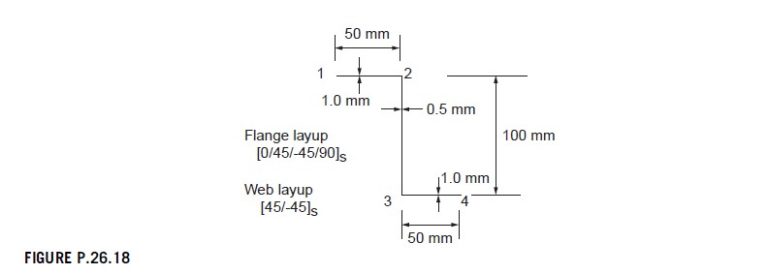
The Z-section beam shown in Fig. P.26.18 carries a bending moment of 0.2 kNm about its X axis. If, for the flanges E_{x}=54,100 N/mm² and for the web Ex=17,700 N/mm², calculate the maximum load intensity in the section.
Learn more on how do we answer questions.
The modified second moments of area are, from Eqs (26.67),
I_{X X}^{\prime}=\int_{A}E_{Z,i}Y^{2}\;\mathrm{d}A,\quad I_{Y Y}^{\prime}=\int_{A}E_{Z,i}X^{2}\;\mathrm{d}A,\quad I_{X Y}^{\prime}=\int_{A}E_{Z,i}X Y\;\mathrm{d}A. (26.67)
I_{X X}^{\prime}=2\times54100\times50\times1\times50^{2}+17700\times0.5\times100^{3}/12=1.43\times10^{10} \mathrm{Nmm^{2}}
In this case M_{Y}=0 so that Eq. (26.68) reduces to
\sigma_{Z}=E_{Z,i}\left[\left({\frac{M_{Y}I_{X X}^{\prime}-M_{X}I_{X Y}^{\prime}}{I_{X X}^{\prime}I_{Y Y}^{\prime}-I_{X Y}^{2}}}\right)X+\left({\frac{M_{X}I_{Y Y}^{\prime}-M_{Y}I_{X Y}^{\prime}}{I_{X X}^{\prime}I_{Y Y}^{\prime}-I_{~X Y}^{2}}}\right)Y\right] (26.68)
\sigma_{Z}=E_{Z,i}\left(\frac{-M_{X}I_{Y Y}^{\prime}X}{I_{X X}^{\prime}I_{Y Y}^{\prime}-(I_{X X}^{\prime})^{2}}+\frac{M_{X}I_{Y Y}^{\prime}Y}{I_{X X}^{\prime}I_{Y Y}^{\prime}-(I_{X Y}^{\prime})^{2}}\right)Substituting the values of M_{X}\,(=\,0.2\,\mathrm{kNm}),\,I_{X X}^{\prime}\;\mathrm{etc.} gives
\sigma_{Z}=E_{Z,1}(0.75X+0.5Y)\times10^{-4}Then, at 1, \sigma_{Z,1}=541000\,[0.75(-50)+0.5\,(50)]\times\;10^{-4}=67.6\;\mathrm{N/mm^{2}} At 2 (in the flange),
\sigma_{Z,2}=54100[0.75(0)+0.5(50)]\times10^{-4}=135.3\,\mathrm{N/mm^{2}}At 2 (in the web),
\sigma_{Z,2}=17700[0.75(0)+0.5(50)]\times10^{-4}=44.3\,\mathrm{N/mm^{2}}At 3 (in the web),
\sigma_{Z.3}=17700[0.75(0)+0.5(-50)]\times10^{-4}=-44.3\,\mathrm{N/mm^{2}}At 3 (in the flange),
\sigma_{Z,3}=54100[0.75(0)+0.5(-50)]\times10^{-4}=-135.3\,\mathrm{N/mm^{2}}At 4,
\sigma_{Z,4}=54100[0.75(0)+0.5(-50)]\times10^{-4}=67.6\,\mathrm{N/mm^{2}}The maximum force intensity is therefore
N({\mathrm{max}}\,)=\pm1\times135.3=135.3\,\mathrm{N/mm}occurring at points 2 and 3 in the flanges.