Question 27.8: A symmetrical panel has the form shown in Fig. P.27.8. The l......
A symmetrical panel has the form shown in Fig. P.27.8. The longerons are of constant area, B_{1} for the edge members and B_{2} for the central member, and the sheet is of uniform thickness t. The panel is assembled without stress. Obtain an expression for the distribution of end load in the central longeron if it is then raised to a temperature T (constant along its length) above the edge members. Also, give the longitudinal displacement, at one end of the panel, of the central longeron relative to the edge members. Assume that end loads are carried only by the longerons, that the sheet carries only shear, and that transverse members are provided to prevent transverse straining and to ensure shear effectiveness of the sheet at the ends of the panel.

Learn more on how do we answer questions.
The panel is symmetrical about its vertical center line, and therefore each half may be regarded as a panel with a built-in end as shown in Fig. S.27.8(a). Further, the panel is symmetrical about its horizontal center line so that only the top half need be considered; the assumed directions of the shear flows are shown.
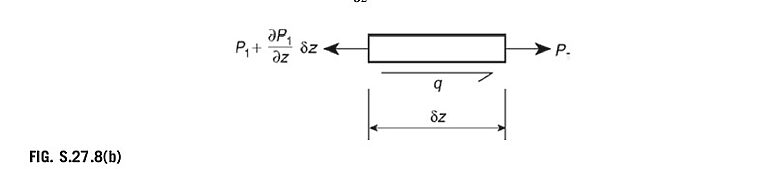
Consider the equilibrium of the element of longeron 1 shown in Fig. S.27.8(b):
P_{1}+{\frac{\partial P_{1}}{\partial z}}\delta z-P_{1}-q\delta z=0Hence,
{\frac{\partial P_{1}}{\partial z}}=q (i)
Now consider the equilibrium of the element of longeron 2 shown in Fig S.27.8(c):
P_{2}+{\frac{\partial P_{2}}{\partial z}}\delta z-P_{2}+2q\delta z=0whence,
{\frac{\partial P_{2}}{\partial z}}=-2q (ii)
From the overall equilibrium of the length z of the panel shown in Fig. S.27.8(d),
2P_{1}+P_{2}=0 (iii)
The compatibility condition for an element of the top half of the panel is shown in Fig. S.27.8(e).
Thus,
i.e.,
{\frac{\mathrm{d}\gamma}{\mathrm{d}z}}={\frac{1}{d}}(\varepsilon_{1}-\varepsilon_{2}) (iv)
In Eq. (iv),
\varepsilon_{1}={\frac{P_{1}}{B_{1}E}}Also, an element, \delta z, of the central longeron would, without restraint, increase in length by an amount \alpha T\,\delta z. The element therefore suffers an effective strain equal to (\epsilon_{2}-\alpha T)\delta z/\delta z. Thus,
{\frac{P_{2}}{B_{2}E}}=\varepsilon_{2}-\alpha Tso that Eq. (iv) becomes
{\frac{\mathrm{d}\gamma}{\mathrm{d}z}}={\frac{1}{d E}}\left({\frac{P_{1}}{B_{1}}}-{\frac{P_{2}}{B_{2}}}-\alpha T E\right)\, (v)
Also γ=q/Gt, and from Eq. (ii), q=-(\partial P_{2}/\partial z)/2. Therefore, substituting for γ and then q in Eq. (v) and for {\mathbf{}}P_{1} from Eq. (iii) in (v),
-{\frac{1}{2}}{\frac{\partial^{2}P_{2}}{\partial z^{2}}}={\frac{G t}{d E}}\left(-{\frac{P_{2}}{2B_{1}}}-{\frac{P_{2}}{B_{2}}}-\alpha T E\right)or
{\frac{\partial^{2}P_{2}}{\partial z^{2}}}-{\frac{2G T}{d E}}\left({\frac{1}{2B_{1}}}+{\frac{1}{B_{2}}}\right)P_{2}={\frac{2G t\alpha T}{d}} (vi)
The solution of Eq. (vi) is
P_{2}=C\cosh\mu z+D\sinh\mu z-{\frac{2G t\alpha T}{\mu^{2}d}} (vii)
where
\begin{array}{c}{{\mu^{2}=\frac{2G t}{d E}\left(\frac{1}{2B_{1}}+\frac{1}{B_{2}}\right)}}\end{array}When z=0, P_{2}{=}0 so that, from Eq. (vii),
C={\frac{2G t a T}{\mu^{2}d}}Also when z=l/2, q=0 and, from Eq. (ii), \partial P_{2}/\partial z=0. Hence, from Eq. (vii),
0=\mu C\sinh\mu{\frac{l}{2}}+\mu D\cosh\mu{\frac{l}{2}}from which
D=-C\mathrm{tanh}\frac{\mu l}{2}=-\frac{2Gt\alpha T}{\mu^{2}d}\mathrm{tanh}\frac{\mu l}{2}Thus,
P_{2}={\frac{2G t\alpha T}{\mu^{2}d}}{\bigg(}{\mathrm{cosh}}\mu z-\operatorname{tanh}{\frac{\mu}{2}}{\mathrm{sinh}}\mu z-1\bigg) (viii)
or, substituting for \mu^{2},
P_2=E \alpha T \frac{\left(\cosh \mu z-\tanh\frac{\mu l}{2} \sinh \mu z-1\right)}{\left(\frac{1}{2B_1}+\frac{1}{B_2}\right)} (ix)
From Fig. S.27.8(e), the relative displacement of the central longeron at one end of the panel is d(\gamma)_{z=0}. Now
\gamma_{z=0}=\left(\frac{q}{G t}\right)_{z=0}=-\frac{1}{2 G t}\left(\frac{\partial P_2}{\partial z}\right)_{z=0} (from Eq.(ii))
Hence, from Eq. (ix),
relative displacement ={\frac{\alpha T}{\mu}}\operatorname{tanh}{\frac{\mu l}{2}}