Question 3.3.4: Find the slope of the line between the points (1, 2) and (3,......
Find the slope of the line between the points (1, 2) and (3, 5).
To find the slope of a line, we can use the formula:
slope = (change in y-coordinates) / (change in x-coordinates)
Step 1:
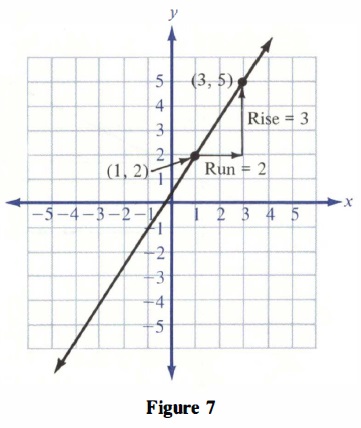
Identify the coordinates of two points on the line. In this case, the given points are (1,2) and (3,5).
Step 2:
Calculate the change in y-coordinates by subtracting the y-coordinate of the first point from the y-coordinate of the second point. In this case, it is 5 - 2 = 3.
Step 3:
Calculate the change in x-coordinates by subtracting the x-coordinate of the first point from the x-coordinate of the second point. In this case, it is 3 - 1 = 2.
Step 4:
Divide the change in y-coordinates by the change in x-coordinates to find the slope. In this case, it is 3/2.
The slope of the line passing through the points (1,2) and (3,5) is 3/2. This means that for every vertical change of 3 units, there will be a corresponding horizontal change of 2 units.
Final Answer
We can let
\left(x_1, y_1\right)=(1,2)
and
\left(x_2, y_2\right)=(3,5)
then
m=\frac{y_2~-~y_1}{x_2~-~x_1}=\frac{5~-~2}{3~-~1}=\frac{3}{2}
The slope is \frac{3}{2}. For every vertical change of 3 units, there will be a corresponding horizontal change of 2 units. (See Figure 7.)
Loading more images...
Related Answered Questions
Question: 3.4.3
Verified Answer:
To identify the slope and y -intercept from the eq...
Question: 3.3.5
Verified Answer:
It makes no difference which ordered pair we call ...
Question: 3.3.PS.1
Verified Answer:
Question: 3.3.PS.3
Verified Answer:
Question: 3.3.PS.5
Verified Answer:
Question: 3.3.PS.7
Verified Answer:
Question: 3.3.PS.9
Verified Answer:
Question: 3.3.PS.11