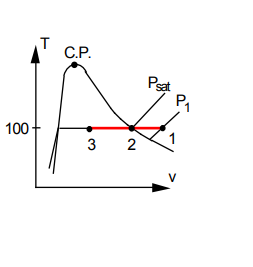
A cylinder having an initial volume of 100 ft^3 contains 0.2 lbm of water at 100 F. The water is then compressed in an isothermal quasi-equilibrium process until it has a quality of 50%. Calculate the work done in the process assuming water vapor is an ideal gas.

Question

A cylinder having an initial volume of 100 [latex]ft ^{3}[/latex] contains 0.2 lbm of water at 100 F. The water is then compressed in an isothermal quasi-equilibrium process until it has a quality of 50%. Calculate the work done in the process assuming water vapor is an ideal gas.

Accepted Answer

State 1: [latex]T _{1}, \quad v _{1}= V / m =\frac{100}{0.2}=500 ft ^{3} / lbm \quad\left(> v _{ g } ight)[/latex]

since [latex]P _{ g }=0.95[/latex] psia, very low so water is an ideal gas from 1 to 2.

[latex]P _{1}= P _{ g } imes \frac{ v _{ g }}{ v _{1}}=0.950 imes \frac{350}{500}=0.6652 lbf / in ^{2}[/latex]

[latex]V _{2}= mv _{2}=0.2 lbm[/latex]*[latex]350 ft ^{3} / lbm =70 ft ^{3}[/latex]

[latex]v _{3}=0.01613+0.5 imes(350-0.01613)=175.0 ft ^{3} / lbm[/latex]

For ideal gas and constant T the work term follows Eq. 3.21

[latex]{ }_{1} W _{2}=\int PdV = P _{1} V _{1} \ln \frac{ V _{2}}{ V _{1}}=0.6652 imes \frac{144}{778} imes 100 \ln \frac{70}{100}=-4.33 Btu[/latex]

For the constant pressure part of the process the work becomes

[latex]{ }_{2} W _{3}= P _{2} m \left( v _{3}- v _{2} ight)=0.95 psi imes 0.2 lbm imes(175-350) ft ^{3} / lbm imes 144 in ^{2} / ft ^{2}[/latex]

= −4788 lbf-ft = −6.15 Btu

[latex]{ }_{1} W _{3}=-6.15-4.33=- 1 0 . 4 8 ~ B t u[/latex]

...........................

Eq.3.21 : [latex]{ }_{1} w _{2}=\frac{P_{2} V_{2}-P_{1} V_{1}}{1-n}[/latex]

Question 3.300E: A cylinder having an initial volume of 100 ft^3 contains 0.2...

Related Answered Questions