A steel wire is wrapped over a block of ice with two heavy weights attached to the ends of the wire. The wire passes through a block of ice without cutting the block in two. The ice melts under the wire and the water freezes again above the wire. The wire is considered a rigid rod of negligible mass laying on the ice block with an area of contact A. The two weights of mass M each are hanging at both ends of the wire (Fig. 6.1). The entire system is at atmospheric pressure p_0 and the ice is held at temperature T_m − ΔT where T_m is the melting temperature at atmospheric pressure. The latent heat of melting of ice is \ell_{s\ell}, the molar volume of water ν_{\ell} and the molar volume of ice is ν_s. Determine the minimal mass M of each weight for this experiment to succeed, i.e. for the wire to pass through the ice block.
Question 6.3: A steel wire is wrapped over a block of ice with two heavy w...
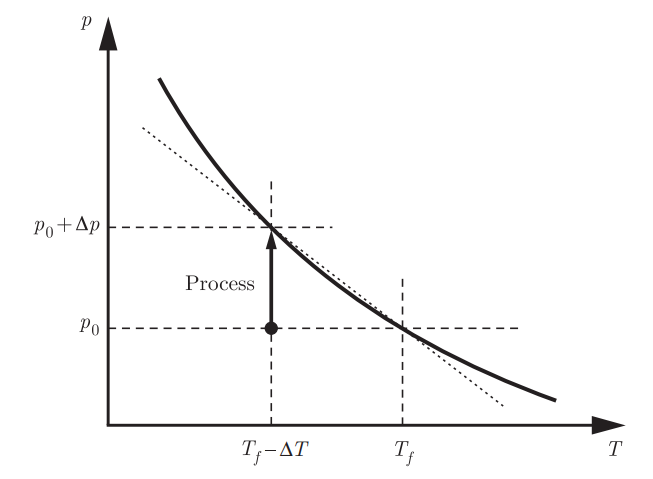
The process of ice melting due to the pressure exerted by the weights is represented by a vertical line on the diagram p (T) (Fig 6.2). The pressure variation Δp between the atmospheric pressure p_0 and the pressure p_0 +Δp at ice melting is expressed on the (p, T) diagram as,
\Delta p = \int_{p_0}^{p_0+\Delta p}{dp} = \int_{T_m}^{T_m -\Delta T}{\frac{dp}{dT} }dT .
Using the Clausius–Clapeyron relation (6.50) where the ice latent heat of melting \ell_{s\ell} is considered as constant, the pressure variation Δp is expressed as, i.e.
\frac{dp}{dT} = \frac{\ell _{s\ell }}{T(\nu _\ell -\nu _s)} and \frac{dp}{dT} = \frac{\ell _{\ell g}}{T(\nu _g -\nu _\ell)} .
\Delta p =- \frac{\ell _{s\ell }}{\nu _s – \nu _\ell } \int_{T_m}^{T_m -\Delta T}{\frac{dT}{T} } = \frac{\ell _{s \ell }}{\nu _s – \nu _\ell } \ln \Bigl(\frac{T_m}{T_m – \Delta T}\Bigr) .
The pressure variation Δp that allows ice to melt is equal to the pressure exerted by the minimal weight of the two masses on the area of contact A between the wire and the ice block,
Δp = \frac{2 M g}{A} .
Equating both expressions for Δp, we obtain the minimal value for the mass M of each weight,
M = \frac{A \ell _{s \ell }}{2 g (\nu _s – \nu _\ell )} \ln \Bigl(\frac{T_m}{T_m -\Delta T}\Bigr) .
