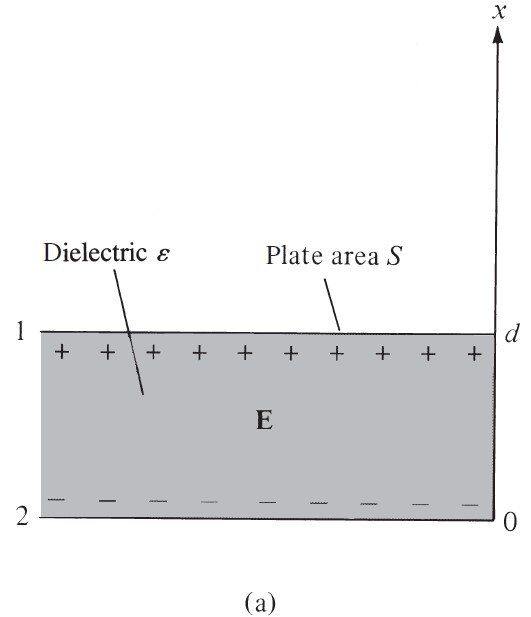
In Section 6.5, it was mentioned that the capacitance C=Q/V of a capacitor can be found by either assuming Q and finding V, as in Section 6.5, or by assuming V and finding Q, as in Example 6.10. Use the latter method to derive eq. (6.22).
C=\frac{Q}{V}=\frac{\varepsilon S}{d}