Find the field outside a uniformly charged solid sphere of radius R and total charge q.

Question

Accepted Answer

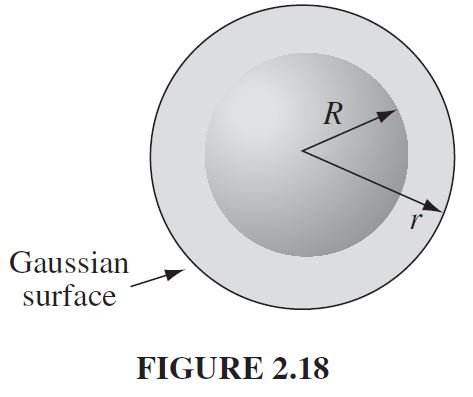
Imagine a spherical surface at radius r > R (Fig. 2.18); this is called a Gaussian surface in the trade. Gauss’s law says that

[latex]\oint\limits_{S}^{}{E.da}=\frac{1}{\varepsilon _{0}}Q_{enc}, [/latex]

and in this case [latex]Q_{enc} = q[/latex]. At first glance this doesn’t seem to get us very far,
because the quantity we want (E) is buried inside the surface integral. Luckily,symmetry allows us to extract E from under the integral sign: E certainly points radially outward,[latex]^{5}[/latex] as does da, so we can drop the dot product,

[latex]\int\limits_{S}^{}{E.da}=\int\limits_{S}^{}{\left|E\right|da} , [/latex]

and the magnitude of E is constant over the Gaussian surface, so it comes outside the integral:

[latex]\int\limits_{S}^{}{\left|E\right| .da}=\left|E\right|\int\limits_{S}^{}{da}=\left|E\right|4\pi r^{2} , [/latex]

Thus

[latex]\left|E\right|4\pi r^{2}=\frac{1}{\varepsilon _{0}}q , [/latex]

or

[latex]E=\frac{1}{4\pi \epsilon_{0} }\frac{q}{r^{2}}\hat{r} [/latex]

Notice a remarkable feature of this result: The field outside the sphere is exactly
the same as it would have been if all the charge had been concentrated at the
center.

Question 2.3: Find the field outside a uniformly charged solid sphere of r...

Related Answered Questions