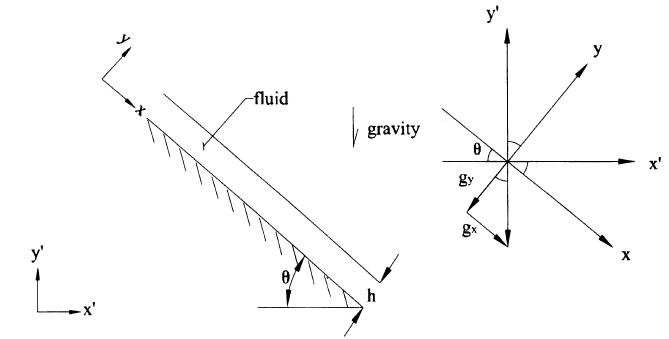
Fluid flow down an inclined plane is influenced by the force of gravity. Consider the flow in Fig. 9.8, where a fluid film is subjected to the effects of gravity alone. Assume that the height of the fluid layer, h, remains constant and that there is no pressure gradient in the x direction. Use the Navier–Stokes equation for steady, incompressible Newtonian flows, given the coordinate system in the figure, to find (a) the pressure distribution in the y direction and (b) the velocity field. FIGURE 9.8 Uniform thickness flow of a Newtonian fluid down an inclined surface. The upper surface of the fluid is exposed to quiescent air at atmospheric pressure (i.e., zero pressure gauge), which is thus called a free surface. The only body force is gravity.
Question 9.3: Fluid flow down an inclined plane is influenced by the force...
Learn more on how we answer questions.
Assume
1. Newtonian fluid (\mu =constant)
2. Incompressible flow (\triangledown \cdot \nu =0)
3. Steady flow (\partial \nu /\partial t=0 )
4. Unidirectional laminar flow (\nu _{y}=\nu _{z}=0)
5. Fully developed flow (\partial \nu /\partial x=0 )
6. 1-D flow (\partial \nu _{x}/\partial z=0, \partial \nu _{x}/\partial x =0 )
7. No pressure gradient in x(\partial p/\partial x =0 )
8. Shear stress due to airflow over the surface of the film is negligible (\sigma _{yx(air)}\approx 0)
The balance of mass, given by Eq. (9.3), is again satisfied identically because \nu =\nu _{x}(y)\hat{i} only. The balance of linear momentum, in Cartesian coordinates, is
\frac{\partial \nu _{x}}{\partial x}+\frac{\partial \nu _{y}}{\partial y}+\frac{\partial \nu _{z}}{\partial z}=0, (9.3)
Some Exact Solutions given by Eqs. (9.4)–(9.6). Given the above assumptions, we again eliminate the
appropriate terms and find that we are left with
=\rho \left(\frac{\partial \nu _{x}}{\partial t}+\nu _{x}\frac{\partial \nu _{x}}{\partial x}+\nu _{y}\frac{\partial \nu _{x}}{\partial y}+\nu _{z}\frac{\partial \nu _{x}}{\partial z} \right), (9.4)
\hat{k}:-\frac{\partial p}{\partial z}+\mu \left(\frac{\partial^{2}\nu_{z}}{\partial x^{2}}+\frac{\partial^{2}\nu_{z}}{\partial y^{2}}+\frac{\partial^{2}\nu_{z}}{\partial z^{2}} \right)+\rho g_{z}
=\rho \left(\frac{\partial \nu _{z}}{\partial t}+\nu _{x}\frac{\partial \nu _{z}}{\partial x}+\nu _{y}\frac{\partial \nu _{z}}{\partial y}+\nu _{z}\frac{\partial \nu _{z}}{\partial z} \right). (9.6)
\mu \frac{\partial ^{2}\nu _{x}}{\partial y^{2}}+\rho g_{x}=0, -\frac{\partial p}{\partial y}+\rho g_{y}=0, -\frac{\partial p}{\partial z}=0,
wherein, due to gravity g=-g\hat{j}^{\prime }, we include the body force acting on the fluid. This force can be resolved into x and y components using the given coordinate systems (remember that coordinate systems should be picked for convenience). Doing so, we see that g_{x}=g\sin \theta and g_{y}=-g\cos \theta Thus, we have
\mu \frac{\partial^{2} \nu _{x}}{\partial y^{2}}+\rho g\sin \theta =0, -\frac{\partial p}{\partial y}-\rho g\cos \theta =0, -\frac{\partial p}{\partial z}=0.Clearly, the pressure is a function of y alone, which can be determined via
\frac{dp}{dy}=-\rho g\cos \theta ,which, upon integration, yields
p(y)=-\rho g(\cos \theta )y+c.Now, we need a boundary condition to solve for the constant c. Knowing that the surface of the fluid film, at y=h, is subjected to atmospheric pressure conditions or P_{atm}, we get
P_{atm}=-\rho g(\cos \theta )h+c\rightarrow c=P_{atm}+\rho g(\cos \theta )h.Thus, the (absolute) pressure distribution in the y direction is
p(y)=\rho g(h-y)\cos \theta +P_{atm}.The gauge pressure is the absolute pressure minus atmospheric pressure. We also see from the x-direction equation of motion that the velocity is a function of y alone, thus the final governing differential equation of motion is
\frac{d^{2}\nu _{x}}{dy^{2}}=-\frac{\rho g\sin \theta }{\mu }.Integrating twice, we obtain
\nu_{x}(y)=-\frac{\rho g\sin \theta }{2\mu }y^{2}+c_{1}y+c_{2}.Invoking the no-slip condition at the face of the inclined plane, \nu _{x}(y=0)=0, we find that
0=0+c_{1}(0)+c_{2}\rightarrow c_{2}=0.Now, we need an appropriate boundary condition for the top surface of the fluid film. Recall that when we formulated the problem, we assumed that the shear stress due to airflow over the fluid film was negligible. Hence,
\sigma _{yx(air)}\approx 0\rightarrow \sigma _{yx(fluid)}\mid _{y=h}=\mu \frac{\partial \nu _{x}}{\partial y}\mid _{y=h}=0,where \sigma _{yx(air)}\mid _{y=h}=-\sigma _{yx(fluid)}\mid _{y=h}. Thus,
\mu \frac{\partial \nu _{x}}{\partial y}\mid _{y=h}=0=\mu \left(-\frac{\rho gh\sin \theta }{\mu }+c_{1} \right),
or
c_{1}=\frac{\rho gh\sin \theta }{\mu }.
Thus, the velocity profile is
\nu _{x}(y)=\frac{\rho g\sin \theta }{\mu }\left(yh-\frac{y^{2}}{2} \right).Once we are finished (i.e., when we have found the velocity and pressure fields), we should always examine special cases, the correctness of which gives us added confidence in our formulation and solution. Note, therefore, that \nu _{x}=0 when \theta =0, as expected, because there is no pressure gradient or moving solid to drive the flow. In conclusion, then, having computed the velocity and pressure fields, we can now calculate any quantity of interest, such as the shear stress, acceleration, or vorticity. This is left as an exercise, however.