Rigid bar ABCD is loaded and supported as shown in Figure P5.65. Bar (1) is made of bronze [E = 100 GPa, α = 16.9 × 10−6/°C] and has a cross-sectional area of 400 mm2 . Bar (2) is made of aluminum [E = 70 GPa, α = 22.5 × 10−6/°C] and has a cross-sectional area of 600 mm2 . Bars (1) and (2) are initially unstressed. After the temperature has increased by 40°C, determine:
(a) the stresses in bars (1) and (2).
(b) the vertical deflection of point A.
Question 5.65: Rigid bar ABCD is loaded and supported as shown in Figure P5...

The Blue Check Mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
Learn more on how we answer questions.
Equilibrium
Consider a FBD of the rigid bar. Assume tension forces in members (1) and (2). A moment equation about pin D gives the best information for this situation:
ΣMD=(3m)F1−(1m)F2=0∴F2=3F1 (a)
Geometry of Deformations Relationship
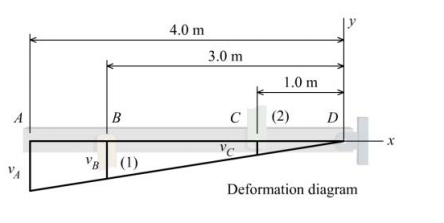
Draw a deformation diagram of the rigid bar. The deflections of the rigid bar are related by similar triangles:
4mvA=3mvB=1mvC (b)
There are no gaps, clearances, or other misfits at pins B and C; therefore, Eq. (b) can be rewritten in terms of the member deformations as:
3m−δ1=1mδ2∴δ1=−3δ2 (c)
Note: To understand the negative sign associated with δ1, see Section 5.5 for discussion of statically indeterminate rigid bar configurations with opposing members.
Force-Temperature-Deformation Relationships
δ1=A1E1F1L1+α1ΔT1L1δ2=A2E2F2L2+α2ΔT2L2 (d)
Compatibility Equation
A1E1F1L1+α1ΔT1L1=−3[A2E2F2L2+α2ΔT2L2] (e)
Solve the Equations
For this situation, ΔT1=ΔT2=ΔT=40∘C . Substitute Eq. (a) into Eq. (e):
and solve for F1:
F1=−A1E1L1+A2E29L2ΔT(3α2L2+α1L1)=−(400 mm2)(100,000 N/mm2)940 mm+(600 mm2)(70,000 N/mm2)9(920 mm)(40∘C)[3(22.5×10−6/∘C)(920 mm)+(16.9×10−6/∘C)(840 mm)]=−13,990 N=−13.990 kNBacksubstitute into Eq. (a) to find F2 = −41.970 kN.
(a) Normal Stresses
The normal stresses in each axial member can now be calculated:
(b) Deflection of the rigid bar at A
Calculate the deformation of one of the axial members, say member (1):
Since there are no gaps at pin B, the rigid bar deflection at B is equal to the deformation of member (1);
therefore, vB=δ1=0.27405mm (upward). From similar triangles, the deflection of the rigid bar at A is related to vB by:
The deflection of the rigid bar at A is thus:
vA=3 m4 mvB=3 m4 m(0.27405 mm)=0.365 mm↑

Related Answered Questions
Equilibrium
Consider a FBD at joint B. Assume that...
Equilibrium
Consider a FBD at joint B. Assume that...
Equilibrium: Consider a FBD of flange B. Sum force...
Equilibrium
Consider a FBD of the rigid bar. Assum...
Equilibrium
Consider a FBD cut through the assembl...
Equilibrium
Consider a FBD of the rigid bar. Assum...
An incremental length dy of the bar has an increme...
(a) Force at base of pile: Consider the entire pil...
Equilibrium
Consider a FBD of joint D. Assume tens...
Equilibrium: The force induced in the bolt by adva...