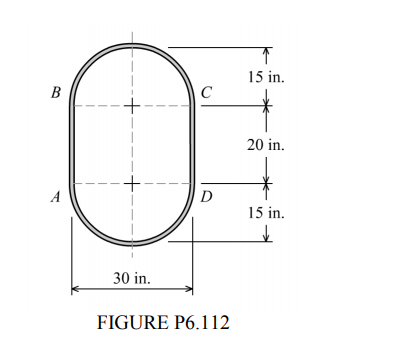
A cross section of an airplane fuselage made of aluminum alloy is shown in Figure P6.112. For an applied torque of T = 1,250 kip-in. and an allowable shear stress of τ = 7.5 ksi, determine the minimum thickness of the sheet (which must be constant for the entire periphery) required to resist the torque. (Note: The dimensions shown are measured to the wall centerline.)
Question 6.112: A cross section of an airplane fuselage made of aluminum all...
The maximum shear stress for a thin-walled section is given by Eq. (6.25)
\tau_{\max }=\frac{T}{2 A_{m} t}For the fuselage,
A_{m}=(30 \text { in. })(20 \text { in. })+\pi(15 \text { in. })^{2}=1,306.858 \text { in. }^{2}The minimum thickness required for the sheet if the maximum shear stress must be limited to 7.5 ksi is thus:
t_{\min }=\frac{T}{2 \tau_{\max } A_{m}}=\frac{1,250 kip – in .}{2(7.5 ksi )\left(1,306.858 in .{ }^{2}\right)}=0.0638 in .
Related Answered Questions
Section properties (from Appendix B)
Depth 300 mm...
Beam equilibrium:
\begin{aligned}&\Sig...
The maximum shear stress for a thin-walled section...
The maximum shear stress for a thin-walled section...
The maximum shear stress for a thin-walled section...
The maximum shear stress for a thin-walled section...
The maximum shear stress for a thin-walled section...
The maximum shear stress for a thin-walled section...
The maximum shear stress for a thin-walled section...