A 1.00-in.-diameter solid steel shaft supports loads $P_{A}$ = 200 lb and $P_{D}$ = 240 lb, as shown in Figure P9.18. Assume $L_{1}$ = 2 in., $L_{2}$ = 5 in., and $L_{3}$ = 4 in. The bearing at B can be idealized as a pin support and the bearing at C can be idealized as a roller support. Determine the magnitude and location of:
(a) the maximum horizontal shear stress in the shaft.
(b) the maximum tension bending stress in the shaft.

Question

A 1.00-in.-diameter solid steel shaft supports loads [latex]P_{A}[/latex] = 200 lb and [latex]P_{D}[/latex] = 240 lb, as shown in Figure P9.18. Assume [latex]L_{1}[/latex] = 2 in., [latex]L_{2}[/latex] = 5 in., and [latex]L_{3}[/latex] = 4 in. The bearing at B can be idealized as a pin support and the bearing at C can be idealized as a roller support. Determine the magnitude and location of:
(a) the maximum horizontal shear stress in the shaft.
(b) the maximum tension bending stress in the shaft.

Accepted Answer

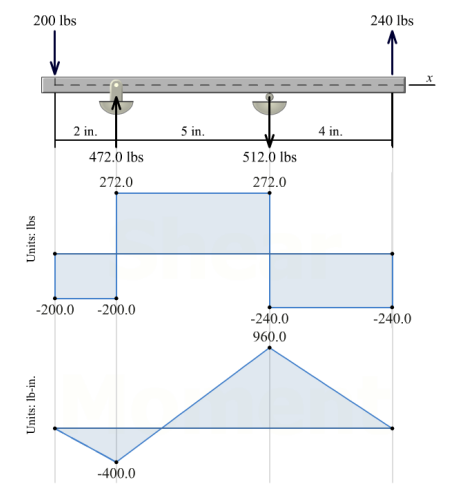
Section properties:

[latex]\begin{aligned}I &=\frac{\pi}{64} D^{4}=\frac{\pi}{64}(1.00 ext { in. })^{4} \&=0.049087 in. ^{4} \Q &=\frac{D^{3}}{12}=\frac{(1.00 in .)^{3}}{12} \&=0.083333 in .^{3}\end{aligned}[/latex]

Maximum shear force magnitude:

[latex]V_{\max }=272 lb ext { (between } B ext { and } C ext { ) }[/latex]

Maximum bending moment magnitude:

[latex]M_{\max }=960 lb - in .( ext { at } C)[/latex]

(a) Maximum horizontal shear stress:

[latex]\begin{aligned} au &=\frac{V Q}{I t}=\frac{(272 lb )\left(0.083333 in.{ }^{3} ight)}{\left(0.049087 in .{ }^{4} ight)(1.00 in .)} \&=461.762 p si =462 psi ext{(at neutral axis between and )}\end{aligned}[/latex]

(b) Maximum tension bending stress:

[latex]\begin{aligned}\sigma_{x} &=-\frac{M y}{I}=-\frac{(960 lb - in .)(-1.00 in . / 2)}{0.049087 in. ^{4}} \&=9,778.480 psi =9,780 psi ( T ) ext{(on bottom of shaft at ) }\end{aligned}[/latex]

Question 9.18: A 1.00-in.-diameter solid steel shaft supports loads PA = 20...

Related Answered Questions