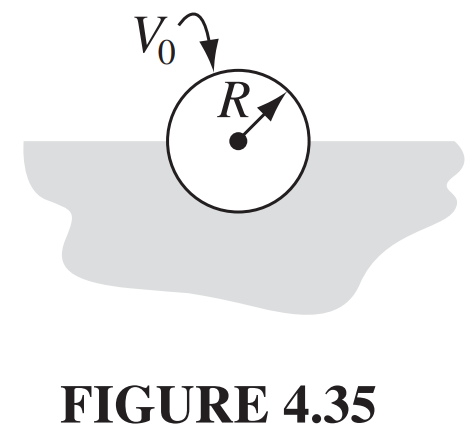
conducting sphere at potential V0 is half embedded in linear dielectric material of susceptibility χe, which occupies the region z

Question

conducting sphere at potential [latex]V_{0}[/latex] is half embedded in linear dielectric material of susceptibility [latex]\chi_{e}[/latex], which occupies the region z < 0 (Fig. 4.35). Claim: the potential everywhere is exactly the same as it would have been in the absence of the dielectric! Check this claim, as follows:

(a) Write down the formula for the proposed potential V (r), in terms of [latex]V_{0}[/latex], R, and r. Use it to determine the field, the polarization, the bound charge, and the free charge distribution on the sphere.

(b) Show that the resulting charge configuration would indeed produce the potential V (r).

(c) Appeal to the uniqueness theorem in Prob. 4.38 to complete the argument.

(d) Could you solve the configurations in Fig. 4.36 with the same potential? If not, explain why

Accepted Answer

(a) Proposed potential: [latex]V(r)=V_{0} \frac{R}{r} . ext { If so, then } E =- abla V=V_{0} \frac{R}{r^{2}} \hat{ r }, ext { in which case } P =\epsilon_{0} \chi_{e} V_{0} \frac{R}{r^{2}} \hat{ r }[/latex] ,

in the region [latex]z<0 .( P =0 ext { for } z>0[/latex] Then [latex] \sigma_b = \epsilon_0 \chi _e V_0\frac{R}{R^2}(\hat{r}. \hat{n})=-\frac{\epsilon_0 \chi_eV_0}{R}[/latex] . (Note: [latex] \hat{n}[/latex] points out of dielectric ⇒ [latex]\hat{n}=-\hat{r}.[/latex] ) This [latex] \sigma_{b}[/latex] is on the surface at r = R. The flat surface z = 0 carries no bound charge, since [latex]\hat{ n }=\hat{ z } \perp \hat{ r }[/latex] . Nor is there any volume bound charge (Eq. 4.39). If V is to have the required spherical symmetry, the net charge must be uniform:

[latex] ho_{b}=- abla \cdot P =- abla \cdot\left(\epsilon_{0} \frac{\chi_{e}}{\epsilon} D ight)=-\left(\frac{\chi_{e}}{1+\chi_{e}} ight) ho_{f}[/latex] (4.39)

[latex]\left.\sigma_{ tot } 4 \pi R^{2}=Q_{ tot }=4 \pi \epsilon_{0} R V_{0} ext { (since } V_{0}=Q_{ tot } / 4 \pi \epsilon_{0} R ight), ext { so } \sigma_{ tot }=\epsilon_{0} V_{0} / R . ext { Therefore }[/latex]

[latex]\sigma_{f}=\left\{\begin{array}{l}\left(\epsilon_{0} V_{0} / R ight), ext { on northern hemisphere } \\left(\epsilon_{0} V_{0} / R ight)\left(1+\chi_{e} ight), ext { on southern hemisphere }\end{array} ight\}[/latex] .

(b) By construction, [latex]\sigma_{ ext {tot }}=\sigma_{b}+\sigma_{f}=\epsilon_{0} V_{0} / R[/latex] is uniform (on the northern hemisphere [latex]\sigma_{b}=0, \sigma_{f}=\epsilon_{0} V_{0} / R [/latex] on the southern hemisphere [latex]\left.\sigma_{b}=-\epsilon_{0} \chi_{e} V_{0} / R, ext { so } \sigma_{f}=\epsilon V_{0} / R ight)[/latex]. The potential of a uniformly charged sphere is

[latex]V_{0}=\frac{Q_{ tot }}{4 \pi \epsilon_{0} r}=\frac{\sigma_{ tot }\left(4 \pi R^{2} ight)}{4 \pi \epsilon_{0} r}=\frac{\epsilon_{0} V_{0}}{R} \frac{R^{2}}{\epsilon_{0} r}=V_{0} \frac{R}{r}[/latex]

(c) Since everything is consistent, and the boundary conditions [latex] \left(V=V_{0} ext { at } r=R, V ightarrow 0 ext { at } \infty ight)[/latex] are met, Prob. 4.38 guarantees that this is the solution.

(d) Figure (b) works the same way, but Fig. (a) does not: on the flat surface, P is not perpendicular to [latex] \hat{ n }[/latex], so we’d get bound charge on this surface, spoiling the symmetry.

Question 4.39: conducting sphere at potential V0 is half embedded in linear...

Related Answered Questions