Determine the location of the shear center O of a thin-walled beam of uniform thickness having the cross section shown in Figures P9.74.

Question

Accepted Answer

Section Properties:

[latex]\begin{aligned}d A &=t d s=t r d heta \quad y=r \sin heta \d I &=y^{2} d A=r^{2} \sin ^{2} heta(t r d heta)=r^{3} t \sin ^{2} heta d heta \I &=r^{3} t \int_{0}^{2 \pi} \sin ^{2} heta d heta \&=r^{3} t \int_{0}^{2 \pi}\left(\frac{1-\cos 2 heta}{2} ight) d heta \&=\pi r^{3} t \d Q &=y d A=r \sin heta(t r d heta)=r^{2} t \sin heta d heta \Q &=r^{2} t \int_{0}^{ heta} \sin heta d heta=r^{2} t(1-\cos heta)\end{aligned}[/latex]

Shear Flow Resultant:

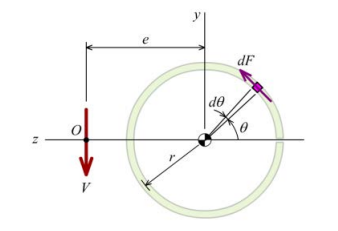
[latex]\begin{aligned}q &=\frac{V Q}{I}=\frac{V r^{2} t(1-\cos heta)}{\pi r^{3} t}=\frac{V}{\pi r}(1-\cos heta) \F &=\int q d s \&=\int_{0}^{2 \pi} \frac{V}{\pi r}(1-\cos heta) r d heta \&=\frac{V}{\pi} \int_{0}^{2 \pi}(1-\cos heta) d heta=2 V\end{aligned}[/latex]

Shear Center: Sum moments about the center of the split tube to find

[latex]\begin{aligned}&V e=F r \&e=\frac{F r}{V}=\frac{2 V r}{V}=2 r\end{aligned}[/latex]

Question 9.74: Determine the location of the shear center O of a thin-walle...

Related Answered Questions