Convert the parallel circuit in Figure 15-49 to a series form.

Question

Accepted Answer

First, find the admittance of the parallel circuit as follows:

[latex]G=\frac{1}{R}= \frac{1}{18 \ k\Omega }= 55.6 \ \mu S[/latex]

[latex]B_{C}=\frac{1}{X_{C}}= \frac{1}{27 \ k\Omega }= 37.0 \ \mu S[/latex]

[latex]Y[/latex] = [latex]G[/latex] + j[latex]B_{C}[/latex] = 55.6 [latex] \mu S[/latex] + 37.0 [latex]\mu S[/latex]

Converting to polar form yields

[latex]Y= \sqrt{G^{2}+ B^{2}_{C}} \angle an ^{-1} \left (\frac{B_{C}}{G} ight) [/latex]

[latex]\ \ \ \ \ = \sqrt{(55.6 \ \mu S)^{2}+ (37.0 \ \mu S)^{2}} \angle an ^{-1} \left(\frac{37.0 \ \mu S}{55.6 \ \mu S} ight)= 66.8 \angle 33.6° \mu S[/latex]

Then, the total impedance is

[latex]Z_{tot}= \frac{1}{Y}=\frac{1}{66.8 \angle 33.6° \mu S}= 15.0 \angle -33.6° \ K\Omega[/latex]

Converting to rectangular form yields

[latex]Z_{tot}= Z\cos heta - jZ\sin heta = R_{eq}- jX_{C(eq)}[/latex]

[latex]\ \ \ \ \ \ = 15.0 \ k\Omega \cos (-33.6°)- j15.0 \ k\Omega \sin (-33.6°)= 12.5 \ k\Omega - j8.31 \ k\Omega [/latex]

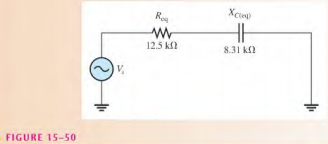
The equivalent series RC circuit is a 12.5 kΩ resistor in series with a capacitive reactance of 8.31 kΩ. This is shown in Figure 15-50.

Question 15.20: Convert the parallel circuit in Figure 15-49 to a series for...

Related Answered Questions