Determine the horizontal displacement of joint A.The members of the truss are A992 steel rods, each having a diameter of 2 in.
Question 14.27: Determine the horizontal displacement of joint A.The members...
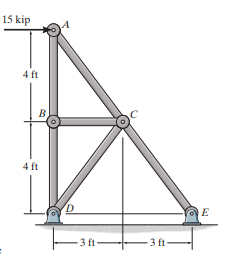
Normal Forces. The normal forces developed in each member of the truss can be determined using method of joints.
Joint A (Fig. a )
Joint B (Fig. b )
\stackrel{+}{\rightarrow} \Sigma F_{x}=0 ; \quad F_{B C}=0 \\+\uparrow \Sigma F_{y}=0 ; \quad 20-F_{B D}=0 \quad F_{B D}=20 \operatorname{kip}( T )Joint C (Fig. c )
+\nearrow \Sigma F_{x^{\prime}}=0 ; \quad F_{C D}=0 \\+\nwarrow \Sigma F_{y^{\prime}}=0 ; \quad F_{C E}-25=0 \quad F_{C E}=25 kip ( C )Axial Strain Energy. A=\frac{\pi}{4}\left(2^{2}\right)=\pi in ^{2} and L_{A C}=L_{C E}=L_{C D}=\sqrt{3^{2}+4^{2}}=5 ft.
\left(U_{i}\right)_{a} =\Sigma \frac{N^{2} L}{2 A E}=\frac{1}{2(\pi)\left[29\left(10^{3}\right)\right]}\left[20^{2}(4)(12)+25^{2}(5)(12)+20^{2}(4)(12)+25^{2}(5)(12)\right] \\=0.6224 in \cdot kipExternal Work. The external work done by the 15 kip force is
U_{e}=\frac{1}{2} P \Delta=\frac{1}{2}(15)\left(\Delta_{h}\right)_{A}=7.5\left(\Delta_{h}\right)_{A}Conservation of Energy.
U_{e}=\left(U_{i}\right)_{a} \\7.5\left(\Delta_{h}\right)_{A}=0.6224 \\\left(\Delta_{h}\right)_{A}=0.08298 \text { in }=0.0830 in
Related Answered Questions
Normal Forces. The normal forces developed in each...
Internal Loadings. Referring to the FBD of beam's ...
Member
n
N
L
nNL
AB
1.25
50
2.5
156.25
AE
-0.7...
member
n
N
L
Nnl
AB
0.6667
3.333
96
2...
member
n
N
L
Nnl
AB
0.6667
3.333
96
213.33
BC
...
member
n
N
L
Nnl
AB
0
0
1.5
0
AC
-1.25
-5
2.5
...
member
n
N
L
Nnl
AB
0
0
1.5
0
AC
0
-5
2.5
0
...
member
n
N
L
Nnl
AB
1.333
18
48
1152
BC
1
15
3...
member
n
N
L(in.)
Nnl
AB
1.333
18
48
1152
BC
0...
Members Real Force N. As indicated in Fig. a .
Mem...