In the high-pressure process for the production of polyethylene, ethylene is compressed in a two-step process. In the primary step, the gas is compressed in a two-stage compressor to 25 to 30 MPa. This is followed by compression in a hyper compressor to 150 to 320 MPa.
Estimate the work required to compress ethylene to 25 MPa in a two-stage compressor. A reciprocating compressor will be used. The gas is at an initial temperature of 15°C and is cooled to 25°C after the first-stage compression.
Question 3.13: In the high-pressure process for the production of polyethyl...
The Blue Check Mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
Learn more on how we answer questions.
As the calculations will be repetitive, use a spreadsheet.
Data T_{in} 288 K P_{in} 1 bar P_{out} 250 ba R = 8.1345 J/mol K
T_{c} 282.4 K P_{c} 50.4 bar M 28.05 C_{p} data from Appendix D
First stage
Intermediate pressure P_{2} = 15.811388 bar eqn 3.39
Compression ratio = P_{2}/P_{1} = 15.814
C_{p} for ethylene T_{in} = 288 use eqn 3.11a
| A | B | C | D |
| Coeff. | 3.806 | 0.15359 | -8.35E-05 | 1.755E-08 |
| C_{p} | 3.806 | 44.23392 | -6.924165 | 0.419256 |
sum,C_{p} = 41.535011 kJ/kmol K
gamma = C_{p}/(C_{p} – R) = 1.2502821
From Figure 3.7, extrapolated, Ep = 0.86.
m = 0.232768 eqn 3.36a
T_{2} = 547.52197 eqn 3.35
Mean temp = (T_{1} + T_{2})/2 = 417.76099
C_{p} at mean temp of 419.6 K
| 3.806 | 0.15359 | – 8.35E-05 | 1.755E-08 |
| 3.806 | 64.446364 | – 14.69784 | 1.2966068 |
sum, C_{p} = 54.851135 kJ/kmol K
new gamma = 1.1786657
revised m = 0.1811049
revised T_{2} = 474.76117
revised mean temp = 381.38058
little change so leave T_{mean} at 419.6 K
T_{r} = T_{mean}/T_{c} = 1.4858357 (1.5)
P_{mean} = (P_{1} * P_{2})/2 = 0.5
P_{t} = P_{mean}/P_{c} = 0.0099206 (0.17)
From Figure 3.2 correction to C_{p} for pressure is negligible.
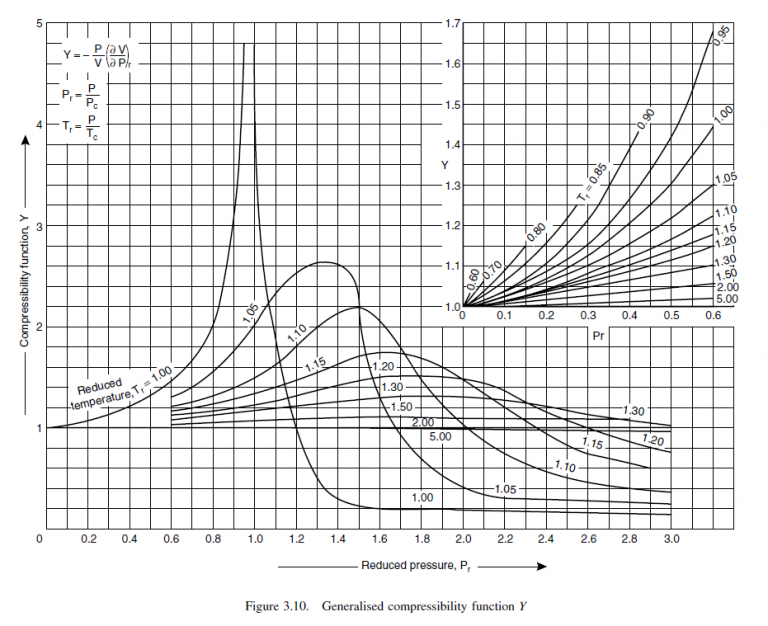
From Figures 3.8, 3.9, 3.10
Z = 1.0 X = 0 Y = 0
Essentially ideal at this pressure
m = 0.1762593 eqn 3.36a
n = 1.2139743 eqn 3.38a
-W = 303.47285 kJ/kmol eqn 3.31
Actual work required = polytropic work/efficiency = 352.87541
Say \underline{\underline{353} } kJ/kmol
Second stage work
As the intermediate pressure was selected to give equal work in each stage the second stage work could be taken as equal to the first stage work. This will be checked.
T_{in} = 298 K
compression ratio = P_{3}/P_{2} = 15.822785, i.e. same as first stage So, take gamma and efficiency as for first stage
m = 0.1811049
T_{3} = 491.24593 K
T_{mean} = 394.62296 K
C_{p} at mean temp
| Coeff. | 3.806 | 0.15359 | -8.35E-05 | 1.755E-08 |
| C_{p} | 3.806 | 60.610141 | -13.00011 | 1.0785715 |
sum, C_{p} = 52.494599 kJ/kmol K
Little change from first stage, so use same gamma and T_{mean}
T_{r} = 1.5
P_{mean} = 20.4 bar
P_{r} = 0.4047619 (0.4)
From Figure 3.2 correction to C_{p} for pressure is approximately 2.5 J/mol.
This is less than 5 per cent, so neglect.
From Figures 3.8, 3.9, 3.10
Z = 1.0 X = 0.1 approx. Y = 0
So, gas can be taken as ideal
-W = 314.01026 slightly higher as T_{in} is higher
Actual work = 365.12821 \underline{\underline{365 kJ/kmol} }
Total work required first step = \underline{\underline{718} } kJ/kmol
The spreadsheet used for this example was Microsoft Works. A copy of the solution using Microsoft Excel can be found on the Butterworth-Heinemann web site: bh.com/companions/ 0750641428.




Related Answered Questions
For the purposes of this calculation it will be su...
The construction of the problem table to find the ...
Component calorific values, from Perry and Chilton...
The rate of heat transfer from the jacket to the w...
Material balance
Basis: 100 kg (as analysis is by ...
From the Mollier diagram, shown diagrammatically i...
For HCl, P_{c} = 82 bar, T_{...
Method 1
Using the more general equation 3.26
[lat...