The shaft depicted in Fig. 11–18a carries a helical gear with a tangential force of 3980 N,a radial force of 1770 N, and a thrust force of 1690 N at the pitch cylinder with directions shown. The pitch diameter of the gear is 200 mm. The shaft runs at a speed of 800 rev/min, and the span

Question

The shaft depicted in Fig. 11–18a carries a helical gear with a tangential force of 3980 N,a radial force of 1770 N, and a thrust force of 1690 N at the pitch cylinder with directions shown. The pitch diameter of the gear is 200 mm. The shaft runs at a speed of 800 rev/min, and the span (effective spread) between the direct-mount bearings is 150 mm. The design life is to be 5000 h and an application factor of 1 is appropriate.If the reliability of the bearing set is to be 0.99, select suitable single-row taperedroller Timken bearings.

Accepted Answer

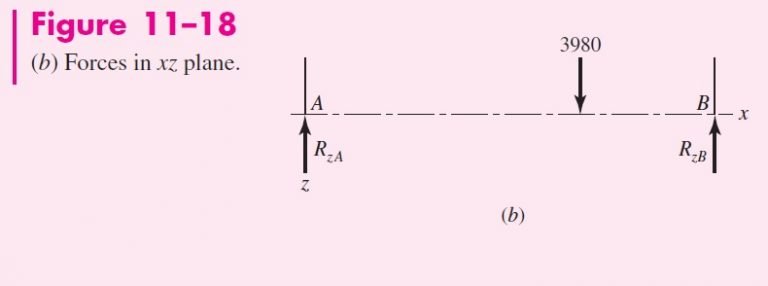
The reactions in the [latex]xz[/latex] plane from Fig. 11–18b are

[latex]R_{zA} = \frac{3980\left(50 ight)}{150}= 1327[/latex] N

[latex]R_{zB} = \frac{3980\left(100 ight)}{150}= 2653[/latex] N

The reactions in the [latex]xy[/latex]plane from Fig. 11–18c are

[latex]R_{yA} = \frac{1770\left(50 ight)}{150}+\frac{169 000)}{150}= 1716.7 = 1717[/latex] N

[latex]R_{yB} = \frac{1770\left(100 ight)}{150}-\frac{169 000)}{150}= 53.3[/latex] N

The radial loads [latex]F_{rA} \ and \ F_{rB}[/latex] are the vector additions of [latex]R_{yA} \ and \ R_{zA} \ , \ and \ R_{yB} \ and \ R_{zB}[/latex] , respectively:

[latex]F_{rA} = \left(R^2_{zA}+ R^2_{yA} ight)^{{1}/{2}} = \left(1327^2 + 1717^2 ight)^{{1}/{2}} = 2170[/latex] N

[latex]F_{rB} = \left(R^2_{zB}+ R^2_{yB} ight)^{{1}/{2}} = \left(2653^2 + 53.3^2 ight)^{{1}/{2}} = 2654[/latex] N

[latex]Trial \ 1[/latex] :With direct mounting of the bearings and application of the external thrust to the shaft, the squeezed bearing is bearing [latex]A[/latex] as labeled in Fig. 11–18a. Using [latex]K[/latex] of 1.5 as the initial guess for each bearing, the induced loads from the bearings are

[latex]F_{iA} = \frac{0.47 F_{rA}}{K_A}= \frac{0.47 \left(2170 ight)}{1.5}= 680[/latex] N

[latex]F_{iB} = \frac{0.47 F_{rB}}{K_B}= \frac{0.47 \left(2654 ight)}{1.5}= 832[/latex] N

Since [latex]F_{iA}[/latex] is clearly less than [latex]F_{iB} + F_{ae}[/latex] , bearing [latex]A[/latex] carries the net thrust load, and Eq. (11–16)

[latex]if \ F_{iA}\leq \left(F_{iB+F_ae} ight) \begin{cases}F_{eA}+0.4 F_{rA}+K_A\left(F _{iB}+F_{ae} ight)\ F_{eB}=F_{rB} \end{cases} [/latex]

is applicable. Therefore, the dynamic equivalent loads are

[latex]F_{eA} = 0.4 F_{rA} + K_A \left(F_{iB} + F_{ae} ight) = 0.4\left(2170 ight) + 1.5\left(832 + 1690 ight) = 4651[/latex] N

[latex]F_{eB} = F_{rB} = 2654[/latex] N

The multiple of rating life is

[latex]x_D = \frac {L_D}{L_R}=\frac{\mathscr{L}_{D} n_{D} 60}{L_R}= \frac {\left(5000 ight)\left(800 ight)\left(60 ight)}{90 \left(106 ight)}= 2.67[/latex]

Estimate [latex]R_D[/latex] as [latex] \sqrt{0.99} = 0.995[/latex] for each bearing. For [latex]A[/latex], from Eq. (11–7) the catalog entry

[latex] C_{10}[/latex] should equal or exceed

[latex]C_{10} = \left(1 ight)\left(4651 ight)\left[ \frac{2.67}{\left(4.48 ight)\left(1-0.995 ight)^{{2}/{3}} } ight]^{{3}/{10}}= 11 486[/latex] N

From Fig. 11–15, tentatively select type TS 15100 cone and 15245 cup, which will work: [latex] K_A = 1.67 \ , \ C_{10} = 12 100[/latex] N.

For bearing [latex]B[/latex] , from Eq. (11–7),

[latex]C_{10} \doteq a_f F_D \left[\frac{x_D}{x_0+\left( heta-x_0 ight)\left(1-R_D ight)^{{1}/{b}} } ight]^{{1}/{a}} \ R \ge 0.90[/latex]

the catalog entry [latex] C_{10}[/latex] should equal or exceed

[latex] C_{10} = \left(1 ight)2654 \left[\frac{2.67}{\left(4.48 ight)\left(1 − 0.995 ight)^{{2}/{3}}} ight]^{{3}/{10}}= 6554 [/latex] N

Tentatively select the bearing identical to bearing [latex]A[/latex], which will work:

[latex] K_B = 1.67 \ , \ C_{10} = 12 100[/latex] N.

[latex]Trial \ 2[/latex]: Repeat the process with [latex] K_A = K_B = 1.67[/latex] from tentative bearing selection.

[latex]F_{iA}= \frac{0.47 F_{rA}}{K_A}=\frac{0.47 \left(2170 ight)}{1.67}= 611[/latex] N

[latex]F_{iB}= \frac{0.47 F_{rB}}{K_B}=\frac{0.47 \left(2654 ight)}{1.67}= 747[/latex] N

Since [latex]F_{iA}[/latex] is still less than [latex]F_{iB} + F_{ae}[/latex] , Eq. (11–16)

is still applicable.

[latex]F_{eA} = 0.4F_{rA} + K_A \left(F{iB} + F_{ae} ight) = 0.4 \left(2170 ight) + 1.67\left(747 + 1690 ight) = 4938[/latex] N

[latex]F_{eB} =F_{rB} = 2654[/latex] N

For [latex]A[/latex], from Eq. (11–7) the corrected catalog entry [latex]C_{10}[/latex] should equal or exceed

[latex]C_{10}= \left(1 ight) \left(4938 ight)\left[\frac{2.67}{\left(4.48 ight)\left(1-0.995 ight)^{{2}/{3}} } ight]^{{3}/{10}} =12195[/latex] N

Although this catalog entry exceeds slightly the tentative selection for [latex]A[/latex], we will keep it since the reliability of bearing [latex]B[/latex] exceeds 0.995. In the next section we will quantitatively show that the combined reliability of [latex]A[/latex] and [latex]B[/latex] will exceed the reliability goal of 0.99. For bearing [latex]B \ , \ F_{eB} = F_{rB} = 2654[/latex] N. From Eq. (11–7),

[latex]C_{10}= \left(1 ight) \left(2654 ight)\left[\frac{2.67}{\left(4.48 ight)\left(1-0.995 ight)^{{2}/{3}} } ight]^{{3}/{10}} = 6554 [/latex] N

Select cone and cup 15100 and 15245, respectively, for both bearing

[latex]A[/latex] and [latex]B[/latex]. Note from Fig. 11–14 the effective load center is located at [latex]a = −5.8[/latex] mm, that is, 5.8 mm into the cup from the back. Thus the shoulder-to-shoulder dimension should be [latex]150 − 2\left(5.8 ight) = 138.4[/latex] mm. Note that in each iteration of Eq. (11–7) to find the catalog load rating, the bracketed portion of the equation is identical and need not be re-entered on a calculator each time.

Question 3.11.8: The shaft depicted in Fig. 11–18a carries a helical gear wit...

This Question has been Answered.

Already have an account?

Login

Related Answered Questions