Reynolds Transport Theorem in Terms of Relative Velocity
Beginning with the Leibniz theorem and the general Reynolds transport theorem for an arbitrarily moving and deforming control volume, Eq. 4–53, prove that Eq. 4–44 is valid.
\frac{d B_{ sys }}{d t}=\int_{ CV } \frac{\partial}{\partial t}(\rho b) d V+\int_{ CS } \rho b \vec{V} \cdot \vec{n} d A (4-53)
\frac{d B_{ sys }}{d t}=\frac{d}{d t} \int_{ CV } \rho b d V+\int_{ CS } \rho b \vec{V}_{r} \cdot \vec{n} d A (4-44)
Equation 4–44 is to be proven.
\frac{d B_{ sys }}{d t}=\frac{d}{d t} \int_{ CV } \rho b d V+\int_{ CS } \rho b \vec{V}_{r} \cdot \vec{n} d A (4-44)
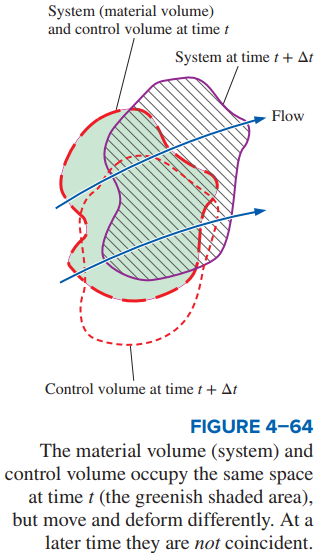
Analysis The general three-dimensional version of the Leibniz theorem, Eq. 4–50, applies to any volume. We choose to apply it to the control volume of interest, which can be moving and/or deforming differently than the material volume (Fig. 4–64). Setting G to 𝜌b, Eq. 4–50 becomes
\frac{d}{d t} \int_{V(t)} G(x, y, z, t) d V=\int_{V(t)} \frac{\partial G}{\partial t} d V+\int_{A(t)} G \vec{V}_{A} \cdot \vec{n} d A (4-50)
\frac{d}{d t} \int_{ CV } \rho b d V =\int_{ CV } \frac{\partial}{\partial t}(\rho b) d V +\int_{ CS } \rho b \vec{V}_{ CS } \cdot \vec{n} d A (1)
We solve Eq. 4–53 for the control volume integral,
\frac{d B_{ sys }}{d t}=\int_{ CV } \frac{\partial}{\partial t}(\rho b) d V+\int_{ CS } \rho b \vec{V} \cdot \vec{n} d A (4-53)
\int_{ CV } \frac{\partial}{\partial t}(\rho b) d V =\frac{d B_{ sys }}{d t}-\int_{ CS } \rho b \vec{V} \cdot \vec{n} d A (2)
Substituting Eq. 2 into Eq. 1, we get
\frac{d}{d t} \int_{ CV } \rho b d V=\frac{d B_{ sys }}{d t}-\int_{ CS } \rho b \vec{V} \cdot \vec{n} d A+\int_{ CS } \rho b \vec{V}_{ CS } \cdot \vec{n} d A (3)
Combining the last two terms and rearranging,
\frac{d B_{ sys }}{d t}=\frac{d}{d t} \int_{ CV } \rho b d V+\int_{ CS } \rho b\left(\vec{V}-\vec{V}_{ CS }\right) \cdot \vec{n} d A (4)
But recall that the relative velocity is defined by Eq. 4–43. Thus,
\vec{V}_{r}=\vec{V}-\vec{V}_{ CS } (4-43)
RTT in terms of relative velocity:
\frac{d B_{ sys }}{d t}=\frac{d}{d t} \int_{ CV } \rho b d V+\int_{ CS } \rho b \vec{V} \cdot \vec{n} d A (5)
Discussion Equation 5 is indeed identical to Eq. 4–44, and the power and elegance of the Leibniz theorem are demonstrated.
\frac{d B_{ sys }}{d t}=\frac{d}{d t} \int_{ CV } \rho b d V+\int_{ CS } \rho b \vec{V}_{r} \cdot \vec{n} d A (4-44)
