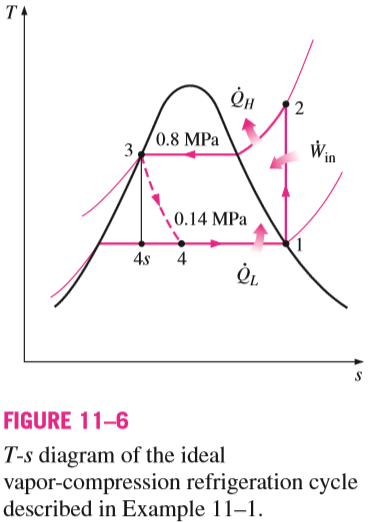
The Ideal Vapor-Compression Refrigeration Cycle
A refrigerator uses refrigerant-134a as the working fluid and operates on an ideal vapor-compression refrigeration cycle between 0.14 and 0.8 MPa. If the mass flow rate of the refrigerant is 0.05 kg/s, determine (a) the rate of heat removal from the refrigerated space and the power input to the compressor, (b) the rate of heat rejection to the environment, and (c) the COP of the refrigerator.
A refrigerator operates on an ideal vapor-compression refrigeration cycle between two specified pressure limits. The rate of refrigeration, the power input, the rate of heat rejection, and the COP are to be determined. Assumptions 1 Steady operating conditions exist. 2 Kinetic and potential energy changes are negligible.
Analysis The T-s diagram of the refrigeration cycle is shown in Fig. 11–6.
We note that this is an ideal vapor-compression refrigeration cycle, and thus the compressor is isentropic and the refrigerant leaves the condenser as a saturated liquid and enters the compressor as saturated vapor. From the refrigerant-134a tables, the enthalpies of the refrigerant at all four states are determined as follows:
\begin{aligned}&\begin{array}{l}P_{1}=0.14 MPa \longrightarrow \\\end{array} \begin{array}{l}h_{1}=h_{g @ 0.14 MPa }=239.16 kJ / kg \\s_{1}=s_{g @ 0.14 MPa }=0.94456 kJ / kg \cdot K\end{array} \\&\left.\begin{array}{l}P_{2}=0.8 MPa \\s_{2}=s_{1}\end{array}\right\} \quad h_{2}=275.39 kJ / kg \\&P_{3}=0.8 MPa \longrightarrow h_{3}=h_{f @ 0.8 MPa }=95.47 kJ / kg \\&h_{4} \cong h_{3} \text { (throttling) } \longrightarrow h_{4}=95.47 kJ / kg\end{aligned}
(a) The rate of heat removal from the refrigerated space and the power input to the compressor are determined from their definitions:
\dot{Q}_{L}=\dot{m}\left(h_{1}-h_{4}\right)=(0.05 kg / s )[(239.16-95.47) kJ / kg ]=7.18 kW
and
\dot{W}_{\text {in }}=\dot{m}\left(h_{2}-h_{1}\right)=(0.05 kg / s )[(275.39-239.16) kJ / kg ]= 1 . 8 1 k W
(b) The rate of heat rejection from the refrigerant to the environment is
\dot{Q}_{H}=\dot{m}\left(h_{2}-h_{3}\right)=(0.05 kg / s )[(275.39-95.47) kJ / kg ]=9.0 kW
It could also be determined from
\dot{Q}_{H}=\dot{Q}_{L}+\dot{W}_{\text {in }}=7.18+1.81=8.99 kW
(c) The coefficient of performance of the refrigerator is
COP _{ R }=\frac{\dot{Q}_{L}}{\dot{W}_{ in }}=\frac{7.18 kW }{1.81 kW }=3.97
That is, this refrigerator removes about 4 units of thermal energy from the refrigerated space for each unit of electric energy it consumes.
Discussion It would be interesting to see what happens if the throttling valve were replaced by an isentropic turbine. The enthalpy at state 4s (the turbine exit with P_{4 s}=0.14 MPa , \text { and } s_{4 s}=s_{3}=0.35404 kJ / kg \cdot K ) is 88.94 kJ/kg, and the turbine would produce 0.33 kW of power. This would decrease the power input to the refrigerator from 1.81 to 1.48 kW and increase the rate of heat removal from the refrigerated space from 7.18 to 7.51 kW. As a result, the COP of the refrigerator would increase from 3.97 to 5.07, an increase of 28 percent.
