Question 9.13: Determine the orbital velocity of a spacecraft at an altitud...

Aircraft performance An Engineering Approach

Determine the orbital velocity of a spacecraft at an altitude of 200 km from the earth if the weightlessness is desired. Assume the gravity is 9.8 m/s² at the height of 200 km and the earth’s radius is 6371 km. Then, compare this velocity with the speed of sound at the sea level (i.e., 340 m/s).

The blue check mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.

$g=\frac{V^2}{R}\Rightarrow 9.8=\frac{V^2}{200,000+6,371,000}\quad \quad \quad \quad (9.173)$

The solution of this equation yields

V=8,025 m/s = 8.02 km/s = 28,889 km/h

This orbital velocity is 23.6 times the speed of sound at sea level.

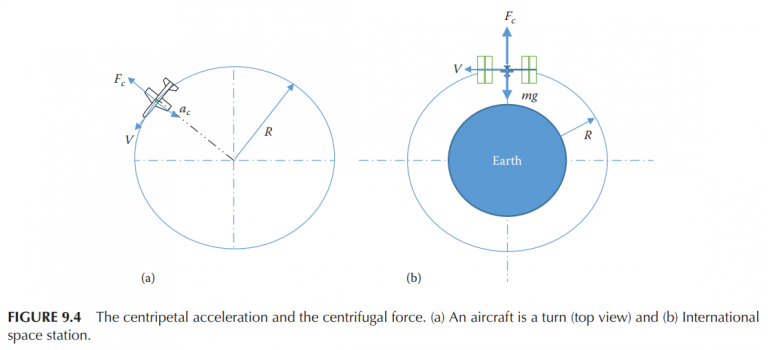
(9.173): $g=\frac{V^2}{R}$ where
m is the mass of the ISS or an astronaut
V is the linear velocity of the ISS or an astronaut
R is the radius of rotation (see Figure 9.4b)

9.4

Related Answered Questions

Question: 9.15

Plot the flight envelope (combined V-n diagram) for the following GA acrobatic aircraft. Then, determine the maximum load factor. m = 2300 kg, S = 19.33 m², CLmax = 2, −CLmax = −1.2, AR = 7, CLα = a = 6.3 1/rad, Vc = 310 KEAS (at 10,000 ft). ...

Verified Answer:

FAR does specify regulations/requirements for gust...

Question: 9.14

An Airbus 300 is employed in a zero-gravity flight. The flight is started at 8000 m with a velocity of 440 knot and lasts about 20 s. Determine (1) horizontal distance traveled, (2) height lost, (3) vertical velocity, (4) average descent angle and (5) total velocity, at the end of 20 s. Ignore the ...

Verified Answer:

The airspeed of 440 knot is equivalent to 226.3 m/...

Question: 9.12

Consider an acrobatic aircraft with a mass of 1500 kg diving with a velocity of 100 knot. a. If the aircraft pulls out of the dive with a radius of 150 m, determine the load factor. b. If the maximum allowable load factor is 6, determine the minimum radius for a pull-out of this dive. ...

Verified Answer:

a. Load factor

n=\frac{V^2}{Rg}+1=\frac{(10...

Question: 9.11

Consider a small remote-controlled (RC) aircraft with the following characteristics: m = 700 g, S = 0.2 m², b = 1 m; e = 0.8; ηP = 0.7, CDo = 0.03, CLmax = 1.2 The airplane is employing a prop-driven electric motor where three cells of 2100 mAh, 12 V Li-Po (lithium polymer) batteries provide ...

Verified Answer:

We first need to find two parameters, namely, AR a...

Question: 9.10

Consider the single-engine piston-prop acrobatic aircraft General Avia F 22 Pinguino with the following features: mTO = 900 kg, S = 10.82 m², P = 130 kW, b = 8.5, Vs = 54 knot (with flap) Assume: CDo = 0.021, ηP = 0.8, e = 0.87. Evaluate the fastest turn performance of this acrobatic aircraft at ...

Verified Answer:

We first need to find three parameters: K, AR, and...

Question: 9.9

A fighter aircraft has the following characteristics: mTO = 25,000 kg, S = 40 m², Tmax = 100 kN, CDo = 0.014; b = 9 m, CLmax = 1.3 Analyze the performance of the aircraft for the tightest turn at two flight conditions for sea level: 1. Theoretical solutions (i.e., application of the maximum engine ...

Verified Answer:

We first need to find two parameters:

AR=\f...

Question: 9.8

Analyze the fastest turn performance for the fighter aircraft McDonnell Douglas (now Boeing) F/A-18 Hornet (Figure 8.12a) at sea level and 50,000 ft altitude (i.e., determine the maximum turn rate). • What are the load factor, bank angle, airspeed, and turn radius for this turn? • Determine the ...

Verified Answer:

From Example 9.6, m = 16,770 kg, S = 38 m², b = 12...

Question: 9.7

Consider the single-engine turboprop utility aircraft Cessna 208 Caravan with the following features: mTO = 3995 kg, S = 25.9 m², P = 647 kW, b = 15.88, Vs = 61 knot, Vmax = 185 knot. Assume: CDo = 0.038, ηP = 0.85, e = 0.9. 1. Determine the corner speed of the aircraft. Then, determine the ...

Verified Answer:

We first need to find two parameters:

AR=\f...

Question: 9.6

Consider the twin-turbofan-engine supersonic, combat aircraft McDonnell Douglas (now Boeing) F/A-18 Hornet (Figure 8.12a) with the following [10] characteristics: m = 16,770 kg, S = 38 m², b = 12.3 m, Tmax = 2 × 79.2 kN Assume the maximum allowable load factor is 10 and αo = 0; CLα = 5 1/rad; ...

Verified Answer:

To investigate the capability of the aircraft for ...

Question: 9.5

A civil subsonic jet (turbojet engine) transport aircraft has the following characteristics: m = 120,000 kg, S = 245 m², TmaxSL = 300 kN, K = 0.06, CDo = 0.02 (low subsonic) The maximum lift coefficient of the aircraft without flap deflection is 1.8.The pilot decides to have a level turn with only ...

Verified Answer:

We first need to find a few parameters:

\Bi...