A column has a solid circular cross section, 1.25 inches in diameter; it has a length of 4.50 ft and is pinned at both ends. If it is made from AISI 1020 cold-drawn steel, what would be a safe column loading?
Question 6.1: A column has a solid circular cross section, 1.25 inches in ...
The Blue Check Mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
Learn more on how we answer questions.
Objective Specify a safe loading for the column.
Given Solid circular cross section: diameter = d = 1.25 in; length = L = 4.50 ft. Both ends of the column are pinned.
Material: AISI 1020 cold-drawn steel.
Analysis Use the procedure in Figure 6-4.
Results Step 1. For the pinned-end column, the end-fixity factor is K = 1.0. The effective length equals the actual length; KL = 4.50 ft = 54.0 in.
Step 2. From Appendix 1, for a solid round section,
| APPENDIX 1 PROPERTIES OF AREAS | |
 |
A = \pi D^4/4 r= D/4 I = \pi D^4/64 J = \pi D^4/32 S = \pi D^3/32 Z_p =\pi D^3/16 |
 |
A = \pi (D^2 – d^2)/4 r = \sqrt{D^2 + d^2} /4 I = \pi (D^4 – d^4)/64 J = \pi (D^4 – d^4)/32 S = \pi (D^4 – d^4)/32D Z_p =\pi (D^4 – d^4)/16D |
 |
A = S^2 r = s/\sqrt{12} I= 5^4/12 S = 5^3/6 |
 |
A = BH r_x = H/\sqrt{12} I_x = BH^3/12 r_y = B/\sqrt{12} S_x = BH^2/6 |
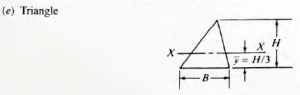 |
A = BH /2 r = H/\sqrt{18} I = BH^3/36 S = BH^2/24 |
 |
A =\pi D^2/8 r= 0.132D I = 0.007D^4 S = 0.024D^3 |
 |
A = 0.866D^2 r = 0.264D I = 0.06D^4 S= 0.12D^3 |
| A = area I = moment of inertia S = section modulus r = radius of gyration = \sqrt{I/A} J = polar moment of inertia Z_p = polar section modulus |
|
r = D/4 = 1.25/4 = 0.3125 in
Step 3. Compute the slenderness ratio:
\frac{KL}{r} =\frac{1.0(54)}{0.3125}= 173
Step 4. Compute the column constant from Equation (6-4). For AISI 1020 cold-drawn steel, the yield strength is 51 000 psi. and the modulus of elasticity is 30 ×10^6 psi. Then
C_c=\sqrt{\frac{2\pi ^2E}{s_y}} =\sqrt{\frac{2\pi ^2(30\times 10^6)}{51000}} = 108
Step 5. Because KL/r is greater than C_c, the column is long, and Euler’s formula should be used. The area is
A=\frac{\pi D^2}{4} =\frac{\pi (1.25)^2}{4}=1.23 \ in^2
Then the critical load is
P_{cr}=\frac{\pi ^2EA}{(KL/r)^2}=\frac{\pi ^2(30\times 10^6) (1.23)}{(173)^2}=12 200 lb
At this load, the column should just begin to buckle. A safe load would be a reduced value, found by applying the design factor to the critical load. Let’s use N= 3 to compute the allowable load, P_a = (12 200)/3=4067 lb
Comment The safe load on the column is 4067 lb.

Related Answered Questions
Objective Specify a suitable diameter for th...
Objective Redesign the eccentrically load...
Objective Specify the allowable load for t...
Objective Compute the critical load for the ...