Acetone is to be recovered from an aqueous waste stream by continuous distillation. The feed will contain 10 per cent w/w acetone. Acetone of at least 98 per cent purity is wanted, and the aqueous effluent must not contain more than 50 ppm acetone. The feed will be at 20ºC. Estimate the number of

Question

Acetone is to be recovered from an aqueous waste stream by continuous distillation. The feed will contain 10 per cent w/w acetone. Acetone of at least 98 per cent purity is wanted, and the aqueous effluent must not contain more than 50 ppm acetone. The feed will be at [latex]20^{\circ} C[/latex]. Estimate the number of ideal stages required.

Accepted Answer

There is no point in operating this column at other than atmospheric pressure. The equilibrium data available for the acetone-water system were discussed in Chapter 8, Section 8.4.

The data of Kojima et al. will be used.

Mol fraction x,liquid	0.00	0.05	0.10	0.15	0.20	0.25	0.30
Acetone y, vapour	0.00	0.6381	0.7301	0.7716	0.7916	0.8034	0.8124
bubble point ŽC	100	74.80	68.53	65.26	63.59	62.60	61.87

x	0.35	0.40	0.45	0.50	0.55	0.60	0.65
y	0.8201	0.8269	0.8376	0.8387	0.8455	0.8532	0.8615
[latex]{ }^{\circ} C[/latex]	61.26	60.75	60.35	59.95	59.54	59.12	58.71

x	0.70	0.75	0.80	0.85	0.90	0.95
y	0.8712	0.8817	0.895	0.9118	0.9335	0.9627
[latex]{ }^{\circ} C[/latex]	58.29	57.90	57.49	57.08	56.68	56.30

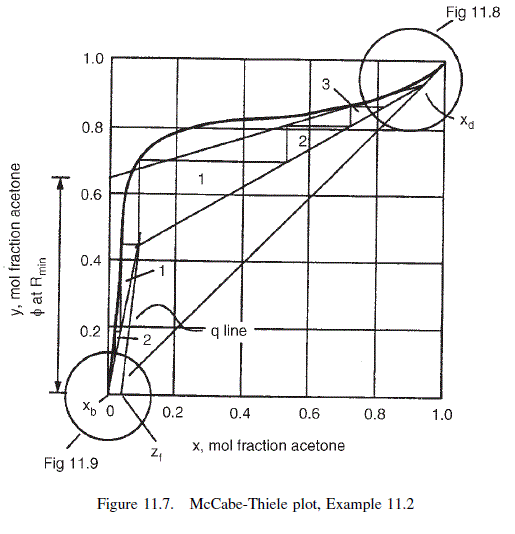
The equilibrium curve can be drawn with sufficient accuracy to determine the stages above the feed by plotting the concentrations at increments of 0.1. The diagram would normally be plotted at about twice the size of Figure 11.7.

Molecular weights, acetone 58, water 18

[latex] ext { Mol fractions acetone feed }=\frac{\frac{10}{58}}{\frac{10}{58}+\frac{90}{18}}=0.033[/latex]

[latex] ext { top product }=\frac{\frac{98}{58}}{\frac{98}{58}+\frac{2}{18}}=0.94[/latex]

[latex] ext { bottom product }=50 imes 10^{-6} imes \frac{18}{58}=15.5 imes 10^{-6}[/latex]

Feed condition (q-line)

Bubble point of feed (interpolated) [latex]=83^{\circ} C[/latex]

Latent heats, water 41,360, acetone 28,410 J/mol

[latex] ext { Mean specific heats, water } 75.3 ext {, acetone } 128 J / mol { }^{\circ} C[/latex]

[latex] ext { Latent heat of feed }=28,410 imes 0.033+(1-0.033) 41,360=40,933 J / mol[/latex]

[latex] ext { Specific heat of feed }=(0.033 imes 128)+(1-0.033) 75.3=77.0 J / mol { }^{\circ} C[/latex]

[latex] ext { Heat to vaporise } 1 mol ext { of feed }=(83-20) 77.0+40,933=45,784 J[/latex]

[latex]q=\frac{45,784}{40,933}=1.12[/latex]

[latex] ext { Slope of } q ext { line }=\frac{1.12}{1.12-1}=9.32[/latex]

For this problem the condition of minimum reflux occurs where the top operating line just touches the equilibrium curve at the point where the q line cuts the curve.

From the Figure 11.7,

[latex]\phi[/latex] for the operating line at minimum reflux = 0.65

[latex] ext { From equation } 11.24, R_{\min }=0.94 / 0.65-1=0.45[/latex]

[latex] ext { Take } R=R_{\min } imes 3[/latex]

As the flows above the feed point will be small, a high reflux ratio is justified; the condenser duty will be small.

[latex] ext { At } R=3 imes 0.45=1.35, \quad \phi=\frac{0.94}{1+1.35}=0.4[/latex]

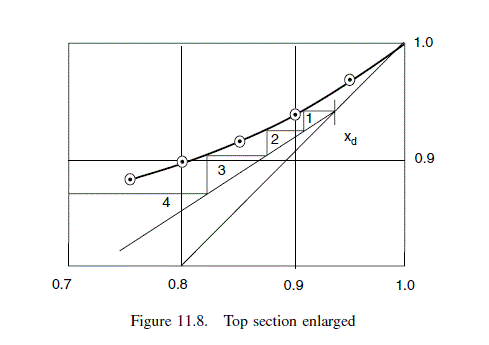
For this problem it is convenient to step the stages off starting at the intersection of the operating lines. This gives three stages above the feed up to y = 0.8. The top section is drawn to a larger scale, Figure 11.8, to determine the stages above y = 0.8: three to four stages required; total stages above the feed 7.

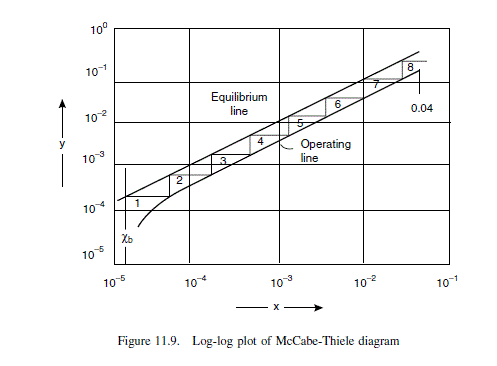
Below the feed, one stage is required down to x = 0.04. A log-log plot is used to determine the stages below this concentration. Data for log-log plot:

operating line slope, from Figure 11.7 = 0.45/0.09 D 5.0

[latex] ext { operating line equation, } y=4.63\left(x-x_{ b } ight)+x_{ b }[/latex] [latex]=5.0 x-62.0 imes 10^{-6}[/latex]

equilibrium line slope, from v l e data = 0.6381/0.05 = 12.8

	x =	[latex]4 imes 10^{-2}[/latex]	[latex]10^{-3}[/latex]	[latex]10^{-4}[/latex]	[latex]4 imes 10^{-5}[/latex]	[latex]2 imes 10^{-5}[/latex]
Equilibrium line	y =	0.51	[latex]1.3 imes 10^{-2}[/latex]	[latex]1.3 imes 10^{-3}[/latex]	[latex]5.1 imes 10^{-4}[/latex]	[latex]2.6 imes 10^{-4}[/latex]
Operating line	y =	0.20	[latex]4.9 imes 10^{-3}[/latex]	[latex]4.4 imes 10^{-4}[/latex]	[latex]1.4 imes 10^{-4}[/latex]	[latex]3.8 imes 10^{-5}[/latex]

From Figure 11.9, number of stages required for this section = 8

Total number of stages below feed = 9

Total stages = 7 + 9 = 16

	x =	$4 \times 10^{-2}$	$10^{-3}$	$10^{-4}$	$4 \times 10^{-5}$	$2 \times 10^{-5}$
Equilibrium line	y =	0.51	$1.3 \times 10^{-2}$	$1.3 \times 10^{-3}$	$5.1 \times 10^{-4}$	$2.6 \times 10^{-4}$
Operating line	y =	0.20	$4.9 \times 10^{-3}$	$4.4 \times 10^{-4}$	$1.4 \times 10^{-4}$	$3.8 \times 10^{-5}$

Question 11.2: Acetone is to be recovered from an aqueous waste stream by c...

Related Answered Questions