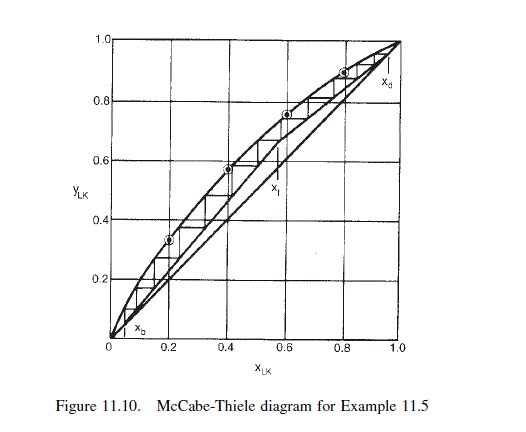
Estimate the number of ideal stages needed in the butane-pentane splitter defined by the compositions given in the table below. The column will operate at a pressure of 8.3 bar, with a reflux ratio of 2.5. The feed is at its boiling point.
Note: a similar problem has been solved by Lyster et al. (1959) using a rigorous computer method and it was found that ten stages were needed.
| Feed (f) | Tops (d) | Bottoms(b) | |
| \text { Propane, } C _{3} | 5 | 5 | 0 |
| \text { i-Butane, } iC _{4} | 15 | 15 | 0 |
| \text { n-Butane, } nC _{4} | 25 | 24 | 1 |
| \text { i-Pentane, } i C _{5} | 20 | 1 | 19 |
| \text { n-Pentane, } nC _{5} | 35 | 0 | 35 |
| 100 | 45 | 55 kmol |