For the plate design in Example 11.11, estimate the plate efficiency for the plate on which the concentration of acetone is 5 mol per cent. Use the AIChE method.
Question 11.12: For the plate design in Example 11.11, estimate the plate ef...
The Blue Check Mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
Learn more on how we answer questions.
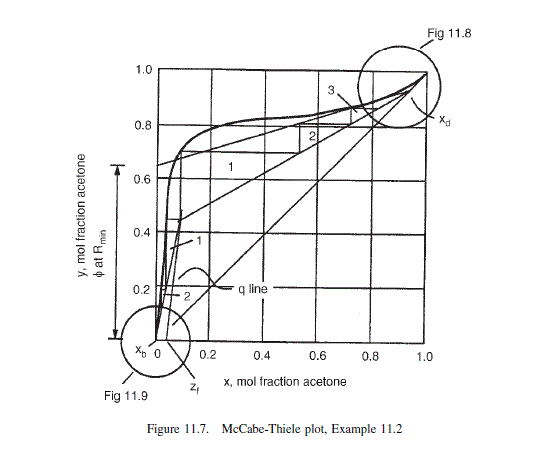
Plate will be in the stripping section (see Figure 11.7).
Plate dimensions:
\text { active area }=0.38 m ^{2}
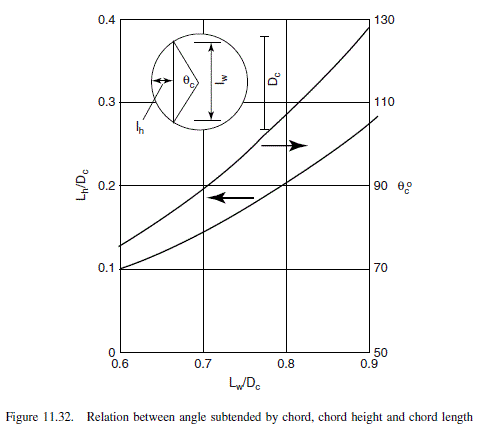
\text { length between downcomers (Figure 11.32) (liquid path, } Z_{L} \text { ) }=0.79-2 \times 0.134= 0.52 m,
weir height = 50 mm.
Flow rates, check efficiency at minimum rates, at column base:
\text { vapour }=0.7 \frac{162.3}{3600}=0.032 kmol / s
\text { liquid }=0.7 \frac{811.6}{3600}=0.158 kmol / s
from the MaCable-Thiele diagram (Figure 11.7) at x = 0.05, assuming 60 per cent plate efficiency, y \approx 0.4. The liquid composition, x = 0.05, will occur on around the ninth plate from the bottom, the seventh from the top of the column. The pressure on this plate will be approximately:
9 \times 138 \times 10^{-3} \times 1000 \times 982+101.4 \times 10^{3}=113.6 kPa
say, 1.14 bar
At this pressure the plate temperature will be 79^{\circ} C, and the liquid and vapour physical properties, from PPDS:
liquid
\text { mol. weight }=20.02, \rho_{L}=925 kg / m ^{3}, \mu_{L}=9.34 \times 10^{-3} Nm ^{-2} s \text {, }
\sigma=60 \times 10^{-3} N / m
vapour
\text { mol. weight }=34.04, \rho_{v}=1.35 kg / m ^{3}, \mu_{v}=10.0 \times 10^{-6} Nm ^{-2} s \text {, }
D_{L}=4.64 \times 10^{-9} m ^{2} / s \text { (estimated using Wilke-Chang equation, Chapter } 8 \text { ) }
D_{v}=18.6 \times 10^{-6} m ^{2} / s \text { (estimated using Fuller equation, Chapter } 8 \text { ) }
\text { Vapour, volumetric flow-rate }=\frac{0.032 \times 34.04}{135}=0.81 m ^{3} / s
\text { Liquid, volumetric flow-rate }=\frac{0.158 \times 20.02}{925}=3.42 \times 10^{-3} m ^{3} / s
u_{a}=\frac{0.81}{0.38}=2.13 m / s
F_{v}=u_{a \sqrt{\rho_{v}}}=\sqrt{2.13} m / s
Average width over active surface = 0.38/0.52 = 0.73 m
L=\frac{3.42 \times 10^{-3}}{0.73}=4.69 \times 10^{-3} m ^{2} / s
N _{G}=\frac{\left(0.776+4.57 \times 10^{-3} \times 50-0.24 \times 2.48+105 \times 4.69 \times 10^{-3}\right)}{\left(\frac{10.0 \times 10^{-6}}{1.35 \times 18.8 \times 10^{-6}}\right)^{1 / 2}} = 1.44 (11.71)
Z_{c}=0.006+0.73 \times 10^{-3} \times 50-0.24 \times 10^{-3} \times 2.48 \times 50+1.22 \times 4.69 \times 10^{-3}=18.5 \times 10^{-3} m ^{3} / m ^{2} (11.75)
t_{L}=\frac{18.5 \times 10^{-3} \times 0.52}{4.69 \times 10^{-3}}=2.05 s (11.73)
N _{L}=\left(4.13 \times 10^{8} \times 4.64 \times 10^{-9}\right)^{0.5} \times(0.21 \times 2.48+0.15) \times 2.05=1.9 (11.72)
D_{e}=\left(0.0038+0.017 \times 2.13+3.86 \times 4.69 \times 10^{-3}+0.18 \times 10^{-3} \times 50\right)^{2} =0.0045 m ^{2} / s (11.77)
P_{e}=\frac{0.52^{2}}{0.0045 \times 2.05}=29.3 (11.76)
From the McCabe-Thiele diagram, at x = 0.05, the slope of the equilibrium line = 1.0.
V/L D 0.032/0.158 = 0.20
\text { so, } \frac{m V}{L}=1.0 \times 0.20=0.20
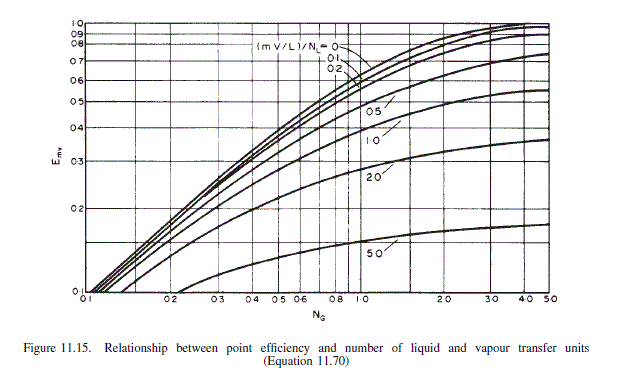
\frac{\left(\frac{m V}{L}\right)}{ N _{L}}=\frac{0.20}{1.9}=0.11
\text { From Figure } 11.15 E_{m v}=0.70
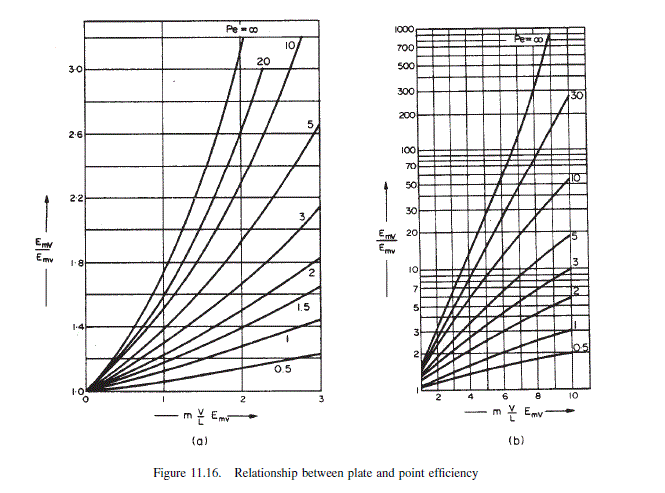
\frac{m V}{L} \cdot E_{m v}=0.2 \times 0.58=0.12
\text { From Figure } 11.16 E_{m V} / E_{m v}=1.02
E_{m V}=0.70 \times 1.02=0.714
So plate efficiency = 71 per cent.
Note: The slope of the equilibrium line is difficult to determine at x = 0.05, but any error will not greatly affect the value of E_{m V}.
Related Answered Questions
As the solubility of SO _{2} in wat...
The top and bottom temperatures (dew points and bu...
From Example 11.5, feed composition, mol fractions...
Only sufficient trial calculations will be made to...
Composition of feed + solvent, point o = 0.45 x 10...
As the liquid and vapour flow-rates and compositio...
From Examples 11.12 and 11.11:
\rho_...
For two phases to exist the flash temperature must...
There is no point in operating this column at othe...
From the McCabe-Thiele diagram in Example 11.2:
sl...