Sulphur dioxide produced by the combustion of sulphur in air is absorbed in water. Pure SO _{2} is then recovered from the solution by steam stripping. Make a preliminary design for the absorption column. The feed will be 5000 kg/h of gas containing 8 per cent v/v SO _{2}. The gas will be cooled to 20^{\circ} C. A 95 per cent recovery of the sulphur dioxide is required.
Question 11.14: Sulphur dioxide produced by the combustion of sulphur in air...
The Blue Check Mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
Learn more on how we answer questions.
As the solubility of SO _{2} in water is high, operation at atmospheric pressure should be satisfactory. The feed-water temperature will be taken as 20^{\circ} C, a reasonable design value.
Solubility data
From Chemical Engineers Handbook, 5th edn, McGraw-Hill, 1973.
| SO _{2} | per cent w/w solution | 0.05 | 0.1 | 0.15 | 0.2 | 0.3 | 0.5 | 0.7 | 1.0 | 1.5 |
| Partial press. gas mmHg | 1.2 | 3.2 | 5.8 | 8.5 | 14.1 | 26 | 39 | 59 | 92 |
\text { Partial pressure of } SO _{2} \text { in the feed }=(8 / 100) \times 760=60.8 mm Hg
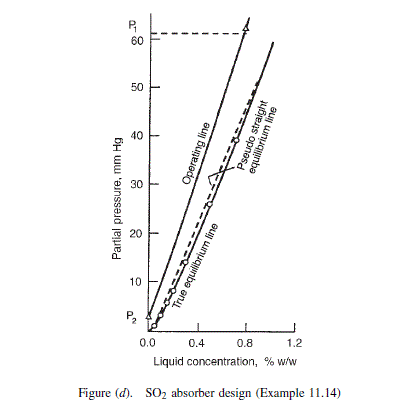
These figures are plotted in Figure (d).
Number of stages
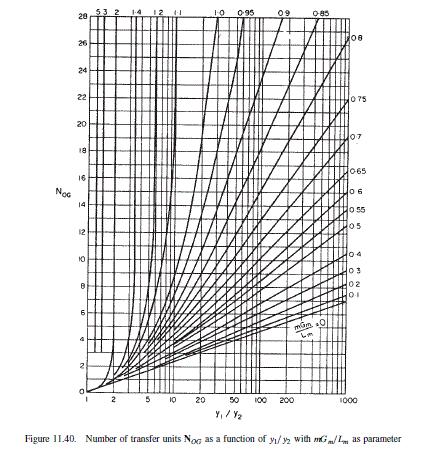
Partial pressure in the exit gas at 95 per cent recovery = 60.8 x 0.05 = 3.04 mm Hg Over this range of partial pressure the equilibrium line is essentially straight so Figure 11.40 can be used to estimate the number of stages needed.
The use of Figure 11.40 will slightly overestimate the number of stages and a more accurate estimate would be made by graphical integration of equation 11.104; but this is not justified in view of the uncertainty in the prediction of the transfer unit height. Molecular weights: SO _{2}=64, H _{2} O =18, \text { air }=29
Slope of equilibrium line
\text { From the data: partial pressure at } 1.0 \% w / w SO _{2}=59 mm Hg \text {. }
\text { Mol. fraction in vapour }=\frac{59}{760}=0.0776
\text { Mol. fraction in liquid }=\frac{\frac{1}{64}}{\frac{1}{64}+\frac{99}{18}}=0.0028
m=\frac{0.0776}{0.0028}=27.4
To decide the most economic water flow-rate, the stripper design should be considered together with the absorption design, but for the purpose of this example the absorption design will be considered alone. Using Figure 11.40 the number of stages required at different water rates will be determined and the “optimum” rate chosen:
\frac{y_{1}}{y_{2}}=\frac{p_{1}}{p_{2}}=\frac{60.8}{3.04}=20
| m \frac{G_{m}}{L_{m}} | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
| N _{O G} | 3.7 | 4.1 | 6.3 | 8 | 10.8 | 19.0 |
It can be seen that the “optimum” will be between m G_{m} / L_{m}= 0.6 to 0.8, as would be expected. Below 0.6 there is only a small decrease in the number of stages required with increasing liquid rate; and above 0.8 the number of stages increases rapidly with decreasing liquid rate.
Check the liquid outlet composition at 0.6 and 0.8:
\text { Material balance } L_{m} x_{1}=G_{m}\left(y_{1}-y_{2}\right)
\text { so } x_{1}=\frac{G_{m}}{L_{m}}(0.08 \times 0.95)=\frac{m}{27.4} \frac{G_{m}}{L_{m}}(0.076)
\text { at } \frac{m G_{m}}{L_{m}}=0.6, x_{1}=1.66 \times 10^{-3} \text { mol fraction }
at \frac{m G_{m}}{L_{m}}=0.8, x_{1}=2.22 \times 10^{-3} \text { mol fraction }
Use 0.8, as the higher concentration will favour the stripper design and operation, without significantly increasing the number of stages needed in the absorber.
N _{O G}=\underline{8}
Column diameter
The physical properties of the gas can be taken as those for air, as the concentration of SO _{2} is low.
\text { Gas flow-rate }=\frac{5000}{3600}=1.39 kg / s ,=\frac{1.39}{29}=0.048 kmol / s
\text { Liquid flow-rate }=\frac{27.4}{0.8} \times 0.048=1.64 kmol / s = 29.5 kg/s.
Select 38 mm \text { ( } \left.1 \frac{1}{2} \text { in. }\right) ceramic Intalox saddles.
\text { From Table } 11.3, F_{p}=170 m ^{-1}
| Table 11.3. Typical packing efficiencies | ||||||
| System | Pressure kPa | Column dia, m | Packing | HTU m | HETP m | |
| type | size, mm | |||||
| Absorption | ||||||
| Hydrocarbons | 6000 | 0.9 | Pall | 50 | 0.85 | |
| NH _{3}- Air – H _{2} O | 101 | _ | Berl | 50 | 0.50 | |
| Air-water | 101 | _ | Berl | 50 | 0.50 | |
| Acetone-water | 101 | 0.6 | Pall | 50 | 0.75 | |
| Distillation | ||||||
| Pentane-propane | 101 | 0.46 | Pall | 25 | 0.46 | |
| IPA-water | 101 | 0.46 | Int. | 25 | 0.75 | 0.50 |
| Methanol-water | 101 | 0.41 | Pall | 25 | 0.52 | |
| 101 | 0.20 | Int. | 25 | 0.46 | ||
| Acetone-water | 101 | 0.46 | Pall | 25 | 0.37 | |
| 101 | 0.36 | Int. | 25 | 0.46 | ||
| Formic acid-water | 101 | 0.91 | Pall | 50 | 0.45 | |
| Acetone-water | 101 | 0.38 | Pall | 38 | 0.55 | 0.45 |
| 101 | 0.38 | Int. | 50 | 0.50 | 0.45 | |
| 101 | 1.07 | Int. | 38 | 1.22 | ||
| MEK-toluene | 101 | 0.38 | Pall | 25 | 0.29 | 0.35 |
| 101 | 0.38 | Int. | 25 | 0.27 | 0.23 | |
| 101 | 0.38 | Pall | 25 | 0.31 | 0.31 | |
| Pall = Pall rings, Berl = Berl saddles, Int. = Intalox saddles | ||||||
\text { Gas density at } 20^{\circ} C =\frac{29}{22.4} \times \frac{273}{293}=1.21 kg / m ^{3}
\text { Liquid density } \simeq 1000 kg / m ^{3}
\text { Liquid viscosity }=10^{-3} Ns / m ^{2}
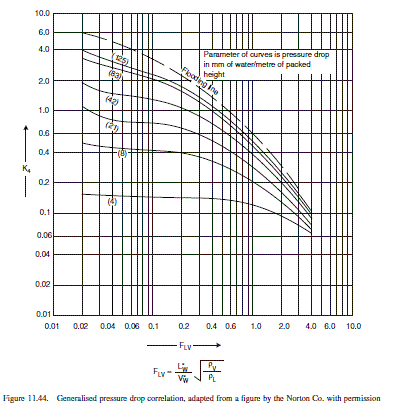
\frac{L_{W}^{*}}{V_{W}^{*}} \sqrt{\frac{\rho_{v}}{\rho_{L}}}=\frac{29.5}{1.39} \sqrt{\frac{1.21}{10^{3}}}=0.74
Design for a pressure drop of 20 mm H _{2} O / m packing
From Figure 11.44,
K_{4}=0.35
\text { At flooding } K_{4}=0.8
\text { Percentage flooding }=\sqrt{\frac{0.35}{0.8}} \times 100=66 \text { per cent, satisfactory. }
From equation 11.118
K_{4}=\frac{13.1\left(V_{w}^{*}\right)^{2} F_{p}\left(\frac{\mu_{L}}{\rho_{L}}\right)^{0.1}}{\rho_{v}\left(\rho_{L}-\rho_{v}\right)} (11.118)
V_{W}^{*}=\left[\frac{K_{4} \rho_{V}\left(\rho_{L}-\rho_{v}\right)}{13.1 F_{p}\left(\mu_{L} / \rho_{L}\right)^{0.1}}\right]^{1 / 2} =\left[\frac{0.35 \times 1.21(1000-1.21)}{13.1 \times 170\left(10^{-3} / 10^{3}\right)^{0.1}}\right]^{1 / 2}=0.87 kg / m ^{2} s
\text { Column area required }=\frac{1.39}{0.87}=1.6 m ^{2}
\text { Diameter }=\sqrt{\frac{4}{\pi}} \times 1.6=1.43 m
Round off to 1.50 m
\text { Column area }=\frac{\pi}{4} \times 1.5^{2}=1.77 m ^{2}
\text { Packing size to column diameter ratio }=\frac{1.5}{38 \times 10^{-3}}=39 \text {, }
A larger packing size could be considered.
Percentage flooding at selected diameter
=66 \times \frac{1.6}{1.77}=60 \text { per cent }
Could consider reducing column diameter.
Estimation of H _{O G}
Cornell’s method
D_{L}=1.7 \times 10^{-9} m ^{2} / s
D_{v}=1.45 \times 10^{-5} m ^{2} / s
\mu_{v}=0.018 \times 10^{-3} Ns / m ^{2}
(S c)_{v}=\frac{0.018 \times 10^{-3}}{1.21 \times 1.45 \times 10^{-5}}=1.04
(S c)_{L}=\frac{10^{-3}}{1000 \times 1.7 \times 10^{-9}}=588
L_{W}^{*}=\frac{29.5}{1.77}=16.7 kg / s m ^{2}
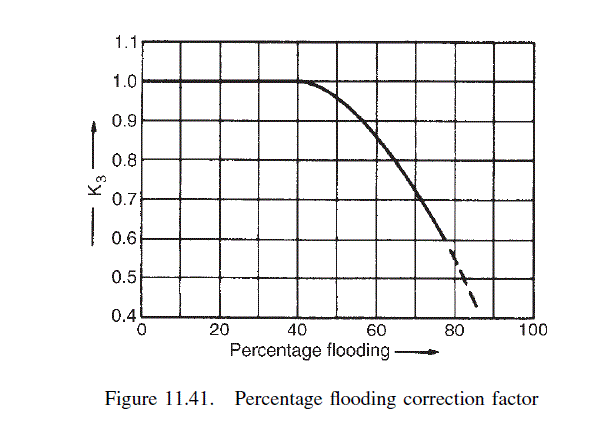
\text { From Figure } 11.41 \text {, at } 60 \text { per cent flooding, } K_{3}=0.85 \text {. }
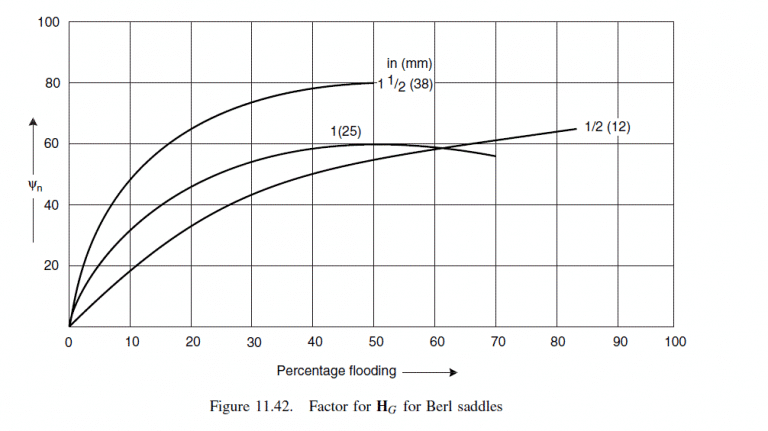
\text { From Figure } 11.42 \text {, at } 60 \text { per cent flooding, } \psi_{h}=80 \text {. }
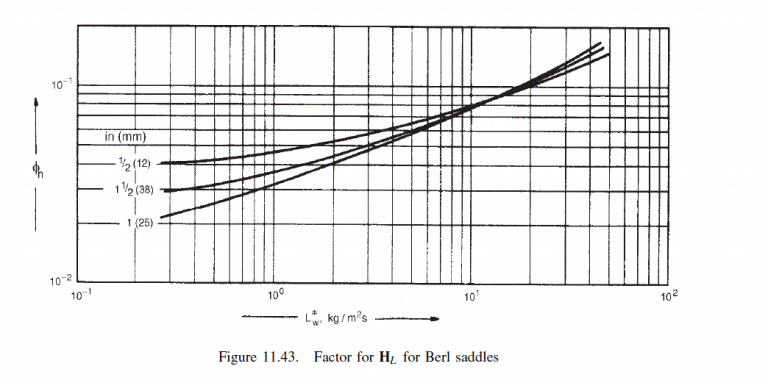
\text { From Figure } 11.43, \text { at } L_{W}^{*}=16.7, \phi_{h}=0.1
H _{O G} can be expected to be around 1 m, so as a first estimate Z can be taken as 8 m. The column diameter is greater than 0.6 m so the diameter correction term will be taken as 2.3.
H _{L}=0.305 \times 0.1(588)^{0.5} \times 0.85\left(\frac{8}{3.05}\right)^{0.15}=0.7 m (11.111)
As the liquid temperature has been taken as 20^{\circ} C, and the liquid is water,.
f_{1}=f_{2}=f_{3}=1
H _{G}=0.011 \times 80(1.04)^{0.5}(2.3)\left(\frac{8}{3.05}\right)^{0.33} /(16.7)^{0.5}=0.7 m (11.110)
H _{O G}=0.7+0.8 \times 0.7=1.3 m (11.105)
Z = 8 x 1.3 = 10.4 m, close enough to the estimated value.
Onda’s method
R =0.08314 \text { bar } m ^{3} / kmol K .
\text { Surface tension of liquid, taken as water at } 20^{\circ} C =70 \times 10^{-3} N / m
g=9.81 m / s ^{2}
d_{p}=38 \times 10^{-3} m
From Table 11.3, for 38 mm Intalox saddles
a=194 m ^{2} / m ^{3}
\sigma_{c} \text { for ceramics }=61 \times 10^{-3} N / m
\frac{a_{W}}{a}=1-\exp \left[-1.45\left(\frac{61 \times 10^{-3}}{70 \times 10^{-3}}\right)^{0.75}\left(\frac{17.6}{194 \times 10^{-3}}\right)^{0.1}\left(\frac{17.6^{2} \times 194}{1000^{2} \times 9.81}\right)^{-0.05}\right. \left.\times\left(\frac{17.6^{2}}{1000 \times 70 \times 10^{-3} \times 194}\right)^{0.2}\right]=0.71 (11.113)
a_{W}=0.71 \times 194=138 m ^{2} / m ^{3}
k_{L}\left(\frac{10^{3}}{10^{-3} \times 9.81}\right)^{1 / 3}=0.0051\left(\frac{17.6}{138 \times 10^{-3}}\right)^{2 / 3}\left(\frac{10^{-3}}{10^{3} \times 1.7 \times 10^{-9}}\right)^{-1 / 2} \times\left(194 \times 38 \times 10^{-3}\right)^{0.4} k_{L}=2.5 \times 10^{-4} m / s (11.114)
V_{W}^{*} \text { on actual column diameter }=\frac{1.39}{1.77}=0.79 kg / m ^{2} s
k_{G} \frac{0.08314 \times 293}{194 \times 1.45 \times 10^{-5}}=5.23\left(\frac{0.79}{194 \times 0.018 \times 10^{-3}}\right)^{0.7} \times\left(\frac{0.018 \times 10^{-3}}{1.21 \times 1.45 \times 10^{-5}}\right)^{1 / 3}\left(194 \times 38 \times 10^{-3}\right)^{-2.0} k_{G}=5.0 \times 10^{-4} kmol / sm ^{2} \text { bar } (11.115)
G_{m}=\frac{0.79}{29}=0.027 kmol / m ^{2} s
L_{m}=\frac{16.7}{18}=0.93 kmol / m ^{2} s
H _{G}=\frac{0.027}{5.0 \times 10^{-4} \times 138 \times 1.013}=0.39 m (11.116)
C_{T}=\text { total concentration, as water, } =\frac{1000}{18}=55.6 kmol / m ^{3}
H _{L}=\frac{0.93}{2.5 \times 10^{-4} \times 138 \times 55.6}=0.49 m (11.117)
H _{O G}=0.39+0.8 \times 0.49=\underline{\underline{\underline{0.78} m }} (11.105)
Use higher value, estimated using Cornell’s method, and round up packed bed height to 11 m.
Related Answered Questions
The top and bottom temperatures (dew points and bu...
From Example 11.5, feed composition, mol fractions...
Only sufficient trial calculations will be made to...
Composition of feed + solvent, point o = 0.45 x 10...
As the liquid and vapour flow-rates and compositio...
Plate will be in the stripping section (see Figure...
From Examples 11.12 and 11.11:
\rho_...
For two phases to exist the flash temperature must...
There is no point in operating this column at othe...
From the McCabe-Thiele diagram in Example 11.2:
sl...