Estimate the heat-transfer coefficient for steam condensing on the outside, and on the inside, of a 25 mm o.d., 21 mm i.d. vertical tube 3.66 m long. The steam condensate rate is 0.015 kg/s per tube and condensation takes place at 3 bar. The steam will flow down the tube.

Question

Accepted Answer

Physical properties, from steam tables:

[latex] ext { Saturation temperature }=133.5^{\circ} C[/latex]

[latex] ho_{L}=931 kg / m ^{3}[/latex]

[latex] ho_{v}=1.65 kg / m ^{3}[/latex]

[latex]k_{L}=0.688 W / m ^{\circ} C[/latex]

[latex]\mu_{L}=0.21 mNs / m ^{2}[/latex]

[latex]P r_{c}=1.27[/latex]

Condensation outside the tube

[latex]\Gamma_{v}=\frac{0.015}{\pi 25 imes 10^{-3}}=0.191 kg / s m[/latex]

[latex]R e_{c}=\frac{4 imes 0.191}{0.21 imes 10^{-3}}=3638[/latex]

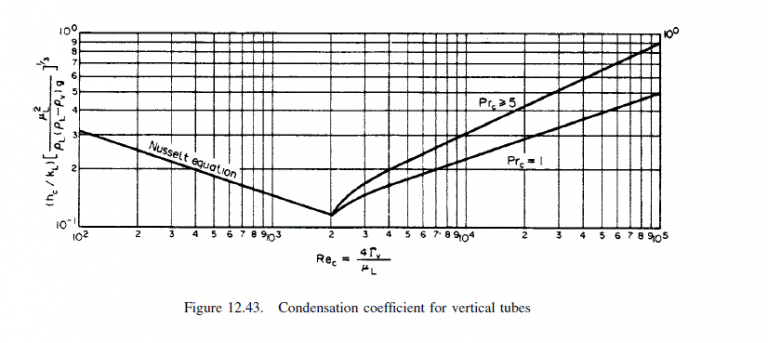
From Figure 12.43

[latex]\frac{h_{c}}{k_{L}}\left[\frac{\mu_{L}^{2}}{ ho_{L}\left( ho_{L}- ho_{v} ight) g} ight]^{1 / 3}=1.65 imes 10^{-1}[/latex]

[latex]\begin{aligned}h_{c} &=1.65 imes 10^{-1} imes 0.688\left[\frac{\left(0.21 imes 10^{-3} ight)^{2}}{931(931-1.65) 9.81} ight]^{-1 / 3} \&=6554 W / m ^{2}{ }^{\circ} C\end{aligned}[/latex]

Condensation inside the tube

[latex]\Gamma_{v}=\frac{0.015}{\pi 21 imes 10^{-3}}=0.227 kg / s m[/latex]

[latex]R e_{c}=\frac{4 imes 0.227}{0.21 imes 10^{-3}}=4324[/latex]

From Figure 12.43

[latex]\begin{aligned}h_{c} &=1.72 imes 10^{-1} imes 0.688\left[\frac{\left(0.21 imes 10^{-3} ight)^{2}}{931(931-1.65) 9.81} ight]^{-1 / 3} \&=6832 W / m ^{2}{ }^{\circ} C\end{aligned}[/latex]

Boyko-Kruzhilin method

[latex] ext { Cross-sectional area of tube }=\left(21 imes 10^{-3} ight)^{2} \frac{\pi}{4}=3.46 imes 10^{-4} m ^{2}[/latex]

Fluid velocity, total condensation

[latex]u_{t}=\frac{0.015}{931 imes 3.46 imes 10^{-4}}=0.047 m / s[/latex]

[latex]R e=\frac{ ho u d_{i}}{\mu_{L}}=\frac{931 imes 0.047 imes 21 imes 10^{-3}}{0.21 imes 10^{-3}}=4376[/latex]

[latex]h_{i}^{\prime}=0.021 imes \frac{0.688}{21 imes 10^{-3}}(4376)^{0.8}(1.27)^{0.43}=624 W / m ^{2}{ }^{\circ} C[/latex] (12.53)

[latex]h_{c}=624\left[\frac{1+\sqrt{931 / 1.65}}{2} ight]=7723 W / m ^{2}{ }^{\circ} C[/latex] (12.54)

[latex] ext { Take higher value, } h_{c}=7723 W / m ^{2}{ }^{\circ} C[/latex]

Question 12.5: Estimate the heat-transfer coefficient for steam condensing ...

Related Answered Questions