Question 7.2: Two pendulums of equal mass and length are connected by a sp...
Two pendulums of equal mass and length are connected by a spiral spring. They vibrate in a plane. The coupling is weak (i.e., the two eigenmodes are not very different). Find the motion with small amplitudes.

Learn more on how we answer questions.
The initial conditions are
x_{1}(0) = 0, x_{2}(0) = A, \dot{x}_{1}(0)= \dot{x}_{2}(0) = 0.We start from the vibrational equation of the simple pendulum:
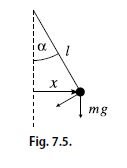
ml\ddot{α} =−mg sin α.
For small amplitudes, we set sinα = α = x/l and obtain
m\ddot{x} =−m \frac{g}{l}x.For the coupled pendulums, the force ∓k(x_{1} −x_{2}) caused by the spring still enters, which leads to the equations
\ddot{x}_{1} =−\frac{g}{l}x_{1} − \frac{k}{m} (x_{1} −x_{2}),\ddot{x}_{2} =−\frac{g}{l}x_{2} + \frac{k}{m} (x_{1} −x_{2}).
This coupled set of differential equations can be decoupled by introducing the coordinates
u_{1} = x_{1} −x_{2} and u_{2} = x_{1} +x_{2}.Subtraction and addition of the equations (7.12) yield
\ddot{u}_{1} =−\frac{g}{l}u_{1} −2 \frac{k}{m} u_{1} =−\left(\frac{g}{l}+ 2 \frac{k}{m}\right)u_{1},\ddot{u}_{2} =−\frac{g}{l}u_{2}.
These two equations can be solved immediately:
u_{1} = A_{1} cos ω_{1}t + B_{1} sin ω_{1}t,
u_{2} = A_{2} cos ω_{2}t + B_{2} sin ω_{2}t, (7.13)
where ω_{1} =\sqrt{g/l +2(k/m)}, ω_{2} =\sqrt{g/l} are the eigenfrequencies of the two vibrations.
The coordinates u_{1}, u_{2} are called normal coordinates. Normal coordinates are often introduced to decouple a coupled system of differential equations. The coordinate u_{1} = x_{1} − x_{2} describes the opposite-phase and u_{2} = x_{1} + x_{2} the equal-phase normal vibration. The equal-phase normal mode proceeds as if the coupling were absent.
For sake of simplicity, we incorporate the initial conditions in (7.13). For the normal coordinates we then have
u_{1}(0)=−A, u_{2}(0) = A, \dot{u}_{1}(0)= \dot{u}_{2}(0) = 0.Insertion into (7.13) yields
A_{1} =−A, A_{2} = A, B_{1} = B_{2} = 0,and thus,
u_{1} =−A cos ω_{1}t, u_{2} = A cos ω_{2}t.Returning to the coordinates x_{1} and x_{2}:
x_{1} = \frac{1}{2} (u_{1} +u_{2}) =\frac{A}{2} (−cos ω_{1}t + cos ω_{2}t),x_{2} = \frac{1}{2} (u_{2} −u_{1}) = \frac{A}{2} (cos ω_{1}t +cos ω_{2}t).
After transforming the angular functions, one has
x_{1} = A sin\left(\frac{ω_{1} −ω_{2}}{2}t\right) sin\left(\frac{ω_{1} +ω_{2}}{2}t\right),x_{2} = A cos\left(\frac{ω_{1} −ω_{2}}{2}t\right) cos\left(\frac{ω_{1} +ω_{2}}{2}t\right),
We have presupposed the coupling of the two pendulums to be weak, i.e.,
ω_{2} =\sqrt{\frac{g}{l}}≈ ω_{1} =\sqrt{\frac{g}{l}+2\frac{k}{m}}hence, the frequency ω_{1} − ω_{2} is small. The vibrations x_{1}(t) and x_{2}(t) can then be interpreted as follows: The amplitude factor of the pendulum vibrating with the frequency ω_{1} +ω_{2} is slowly modulated by the frequency ω_{1} −ω_{2}. This process is called beat vibration. Figure 7.6 illustrates the process. The two pendulums exchange their energy with the amplitude modulation frequency ω_{1} − ω_{2}. If one pendulum reaches its maximum amplitude (energy), the other pendulum comes to rest. This complete energy transfer occurs only for identical pendulums. If the pendulums differ in mass or length, the energy transfer becomes incomplete; the pendulums vary in amplitudes but without coming to rest.