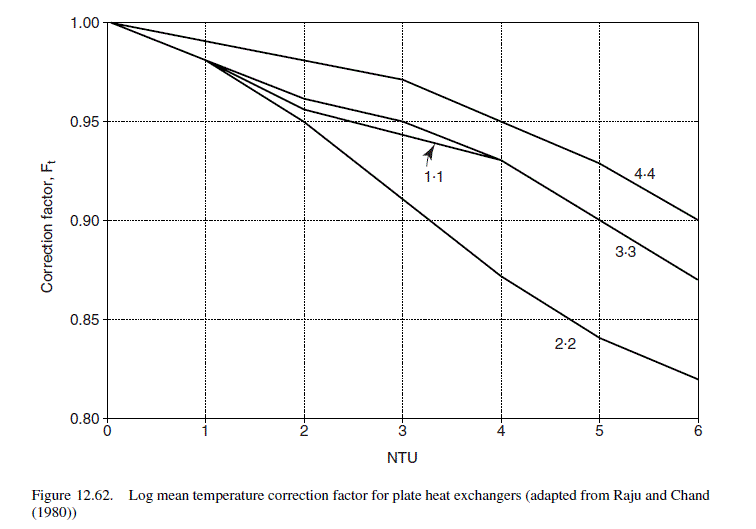
NTU, based on the maximum temperature difference
=\frac{95-40}{31}=1.8
Try a 1 : 1 pass arrangement.
\text { From Figure } 12.62, F_{t}=0.96
From Table 12.2 take the overall coefficient, light organic – water, to be 2000 m ^{-20} C ^{-1}.
| Table 12.2. Fouling factors (coefficients), typical values |
| Fluid |
\text { Coefficient }\left( W / m ^{2}{ }^{\circ} C \right) |
\text { Factor (resistance) }\left( m ^{2 \circ} C / W \right) |
| River water |
3000-12,000 |
0.0003-0.0001 |
| Sea water |
1000-3000 |
0.001-0.0003 |
| Cooling water (towers) |
3000-6000 |
0.0003-0.00017 |
| Towns water (soft) |
3000-5000 |
0.0003-0.0002 |
| Towns water (hard) |
1000-2000 |
0.001-0.0005 |
| Steam condensate |
1500-5000 |
0.00067-0.0002 |
| Steam (oil free) |
4000-10,000 |
0.0025-0.0001 |
| Steam (oil traces) |
2000-5000 |
0.0005-0.0002 |
| Refrigerated brine |
3000-5000 |
0.0003-0.0002 |
| Air and industrial gases |
5000-10,000 |
0.0002-0.0001 |
| Flue gases |
2000-5000 |
0.0005-0.0002 |
| Organic vapours |
5000 |
0.0002 |
| Organic liquids |
5000 |
0.0002 |
| Light hydrocarbons |
5000 |
0.0002 |
| Heavy hydrocarbons |
2000 |
0.0005 |
| Boiling organics |
2500 |
0.0004 |
| Condensing organics |
5000 |
0.0002 |
| Heat transfer fluids |
5000 |
0.0002 |
| Aqueous salt solutions |
3000-5000 |
0.0003-0.0002 |
\text { Then, area required }=\frac{4340 \times 10^{3}}{2000 \times 0.96 \times 31}=72.92 m ^{2}
Select an effective plate area of 0.75 m ^{2}, effective length 1.5 m and width 0.5 m; these are typical plate dimensions. The actual plate size will be larger to accommodate the gasket area and ports.
Number of plates = total heat transfer area / effective area of one plate
= 72.92/0.75 = 97
No need to adjust this, 97 will give an even number of channels per pass, allowing for an end plate.
Number of channels per pass = (97 – 1)/2 = 48
Take plate spacing as 3 mm, a typical value, then:
\text { channel cross-sectional area }=3 \times 10^{-3} \times 0.5=0.0015 m ^{2}
\text { and hydraulic mean diameter }=2 \times 3 \times 10^{-3}=6 \times 10^{-3} m
Methanol
\text { Channel velocity }=\frac{27.8}{750} \times \frac{1}{0.0015} \times \frac{1}{48}=0.51 m / s
R e=\frac{\rho u_{p} d_{e}}{\mu}=\frac{750 \times 0.51 \times 6 \times 10^{-3}}{0.34 \times 10^{-3}}=6750
N u=0.26(6750)^{0.65} \times 5.1^{0.4}=153.8 (12.77)
h_{p}=153.8\left(0.19 / 6 \times 10^{-3}\right)=4870 Wm ^{-2{ }^{\circ} C ^{-1}}
Brackish water
\text { Channel velocity }=\frac{68.9}{995} \times \frac{1}{0.0015} \times \frac{1}{48}=0.96 m / s
R e=\frac{955 \times 0.96 \times 6 \times 10^{-3}}{0.8 \times 10^{-3}}=6876
N u=0.26(6876)^{0.65} \times 5.7^{0.4}=162.8 (12.77)
h_{p}=162.8\left(0.59 / 6 \times 10^{-3}\right)=16,009 Wm ^{-2} C ^{-1}
Overall coefficient
From Table 12.9, take the fouling factors (coefficients) as: brackish water (seawater) 6000 Wm ^{-20} C ^{-1} and methanol (light organic) 10,000 Wm ^{-20} C ^{-1}.
| Table 12.9. Fouling factors (coefficients), typical values for plate heat exchangers |
| Fluid |
\text { Coefficient }\left( W / m ^{2}{ }^{\circ} C \right) |
\text { Factor }\left( m ^{2} C / W \right) |
| Process water |
30,000 |
0.00003 |
| Towns water (soft) |
15,000 |
0.00007 |
| Towns water (hard) |
6000 |
0.00017 |
| Cooling water (treated) |
8000 |
0.00012 |
| Sea water |
6000 |
0.00017 |
| Lubricating oil |
6000 |
0.00017 |
| Light organics |
10,000 |
0.0001 |
| Process fluids |
5000-20,000 |
0.0002-0.00005 |
Take the plate thickness as 0.75 mm. Thermal conductivity of titanium 21 Wm ^{-20} C ^{-1}.
\begin{array}{c}\frac{1}{U}=\frac{1}{4870}+\frac{1}{10,000}+\frac{0.75 \times 10^{-3}}{21}+\frac{1}{16,009}+\frac{1}{6000} \\U=1754 Wm ^{-2 \circ} C ^{-1}, \text { too low }\end{array}
Increase the number of channels per pass to 60; giving (2 ð 60) + 1 = 121 plates.
\text { Then, methanol channel velocity }=0.51 \times(48 / 60)=0.41 m / s \text {, and } \operatorname{Re}=5400 \text {. }
\text { Cooling water channel velocity }=0.96 \times(48 / 60)=0.77 m / s \text {, and } R e=5501
\text { Giving, } h_{p}=4215 Wm ^{-2 \circ} C ^{-1} \text { for methanol, and } 13,846 Wm ^{-2 \circ} C ^{-1} \text { for water. }
\text { Which gives an overall coefficient of } \underline{1634} Wm ^{-2 \circ} C ^{-1} \text {. }
\text { Overall coefficient required } 2000 \times 48 / 60=\underline{\underline{1600}} Wm ^{-2{ }^{\circ} C ^{-1}} \text {, so } 60 \text { plates per pass }
should be satisfactory.
Pressure drops
Methanol
J_{f}=0.60(5400)^{-0.3}=0.046
Path length = plate length x number of passes = 1.5 x 1 = 1.5 m.
\Delta P_{p}=8 \times 0.046\left(\frac{1.5}{6 \times 10^{-3}}\right) \times 750 \times \frac{0.41^{2}}{2}=5799 N / m ^{2} (12.78)
Port pressure loss, take port diameter as 100 mm, area = 0.00785 m ^{2}.
Velocity through port = (27.8/750)/0.00785 = 4.72 m/s.
\Delta P_{p t}=1.3 \times \frac{750 \times 4.72^{2}}{2}=10,860 N / m ^{2} (12.79)
\text { Total pressure drop }=5799+10,860=16,659 N / m ^{2}, 0.16 \text { bar. }
Water
J_{f}=0.6(5501)^{-0.3}=0.045
Path length = plate length x number of passes = 1.5 x 1 = 1.5 m.
\Delta P_{p}=8 \times 0.045 \times\left(\frac{1.5}{6 \times 10^{-3}}\right) \times 995 \times \frac{0.77^{2}}{2}=26,547 N / m ^{2} (12.78)
Velocity through port = (68.9/995)/0.0078 = 8.88 m/s (rather high)
\Delta P_{p t}=1.3 \times \frac{995 \times 8.88}{2}=50,999 N / m ^{2}
\text { Total pressure drop }=26,547+50,999=77,546 N / m ^{2}, 0.78 bar
Could increase the port diameter to reduce the pressure drop.
The trial design should be satisfactory, so a plate heat exchanger could be considered for this duty.