Question 9.14: A cantilever beam ACB having a length L and two different mo...
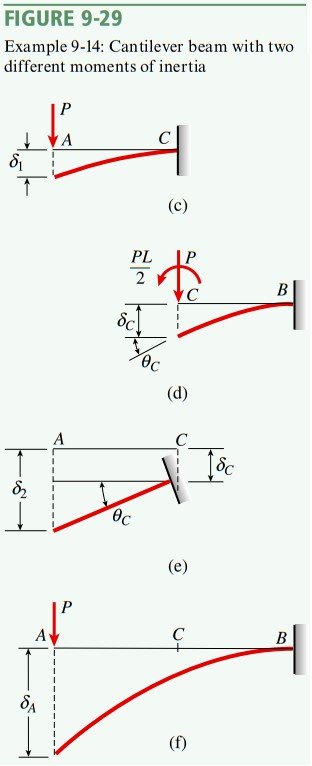
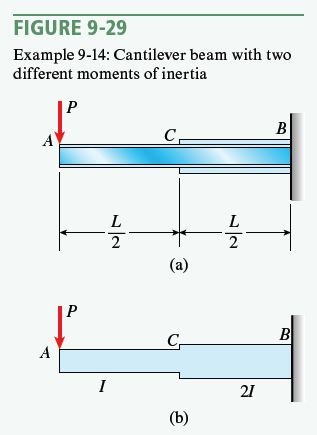
A cantilever beam ACB having a length L and two different moments of inertia I and 2I supports a concentrated load P at the free end A (Figs. 9-29a and b). Determine the deflection δ_{A} at the free end.
Learn more on how we answer questions.
Use a four-step problem-solving approach.
1. Conceptualize: In this example, use the method of superposition to determine the deflection \delta_{A} at the end of the beam. Begin by recognizing that the deflection consists of two parts: the deflection due to bending of part AC of the beam and the deflection due to bending of part CB. Find these deflections separately and then superpose them to obtain the total deflection.
2. Categorize:
Deflection due to bending of part AC of the beam: Imagine that the beam is held rigidly at point C, so that the beam neither deflects nor rotates at that point (Fig. 9-29c). Now calculate the deflection \delta_{1} of point A in this beam. Since the beam has length L/2 and moment of inertia I, its deflection (see Case 4 of Table H-1, Appendix H) is
\delta_{1}=\frac{P(L / 2)^{3}}{3 E I}=\frac{P L^{3}}{24 E I} (a)
Deflection due to bending of part CB of the beam: Part CB of the beam also behaves as a cantilever beam (Fig. 9-29d) and contributes to the deflection of point A. The end of this cantilever is subjected to a concentrated load P and a moment PL/2. Therefore, the deflection \delta_{C} and angle of rotation \theta_{C} at the free end (Fig. 9-29d) are (see Cases 4 and 6 of Table H-1):
\delta_{C}=\frac{P(L / 2)^{3}}{3(2 E I)}+\frac{(P L / 2)(L / 2)^{2}}{2(2 E I)}=\frac{5 P L^{3}}{96 E I}\theta_{C}=\frac{P(L / 2)^{2}}{2(2 E I)}+\frac{(P L / 2)(L / 2)}{2 E I}=\frac{3 P L^{2}}{16 E I}
This deflection and angle of rotation make an additional contribution \delta_{2} to the deflection at end A (Fig. 9-29e). Again visualize part AC as a cantilever beam, but now its support (at point C) moves downward by the amount \delta_{C} and rotates counterclockwise through the angle \theta_{C} (Fig. 9-29e). These rigid-body displacements produce a downward displacement at end A equal to
\delta_{2}=\delta_{C}+\theta_{C}\left(\frac{L}{2}\right)=\frac{5 P L^{3}}{96 E I}+\frac{3 P L^{2}}{16 E I}\left(\frac{L}{2}\right)=\frac{7 P L^{3}}{48 E I} (b)
Total deflection: The total deflection \delta_{A} at the free end A of the original cantilever beam (Fig. 9-29f) is equal to the sum of the deflections \delta_{1} and \delta_{2}:
\delta_{A}=\delta_{1}+\delta_{2}=\frac{P L^{3}}{24 E I}+\frac{7 P L^{3}}{48 E I}=\frac{3 P L^{3}}{16 E I} (9-90)
4. Finalize: This example illustrates one of the many ways that the principle of superposition may be used to find beam deflections.
| Table H-1 | |
| Deflections and Slopes of Cantilever Beams | |
 |
Notation: |
| v = deflection in the y direction (positive upward) | |
| v′ = dv/dx = slope of the deflection curve | |
| \delta_{B}=-v(L)= deflection at end B of the beam (positive downward) | |
| \theta_{B}=-v^{\prime}(L)= angle of rotation at end B of the beam (positive clockwise) | |
| EI = constant | |

|
v=-\frac{q x^{2}}{24 E I}\left(6 L^{2}-4 L x+x^{2}\right) \quad v^{\prime}=\frac{q x}{6 E I}\left(3 L^{2}-3 L x+x^{2}\right) |
| \delta_{B}=\frac{q L^{4}}{8 E I} \quad \theta_{B}=\frac{q L^{3}}{6 E I} | |
 |
v=-\frac{q x^{2}}{24 E I}\left(6 a^{2}-4 a x+x^{2}\right) \quad(0 \leq x \leq a) |
| v^{\prime}=-\frac{q x}{6 E I}\left(3 a^{2}-3 a x+x^{2}\right) \quad(0 \leq x \leq a) | |
| v=-\frac{q a^{3}}{24 E I}(4 x-a) \quad v^{\prime}=-\frac{q a^{3}}{6 E I} \quad(a \leq x \leq L) | |
| At x=a: v=-\frac{q a^{4}}{8 E I} \quad v^{\prime}=-\frac{q a^{3}}{6 E I} | |
| \delta_{B}=\frac{q a^{3}}{24 E I}(4 L-a) \quad \theta_{B}=\frac{q a^{3}}{6 E I} | |
 |
v=-\frac{q b x^{2}}{12 E I}(3 L+3 a-2 x) (0 \leq x \leq a) |
| v^{\prime}=-\frac{q b x}{2 E I}(L+a-x) (0 \leq x \leq a) | |
| v=-\frac{q}{24 E I}\left(x^{4}-4 L x^{3}+6 L^{2} x^{2}-4 a^{3} x+a^{4}\right) \quad(a \leq x \leq L) | |
| v^{\prime}=-\frac{q}{6 E I}\left(x^{3}-3 L x^{2}+3 L^{2} x-a^{3}\right) \quad(a \leq x \leq L) | |
| At x=a: v=-\frac{q a^{2} b}{12 E I}(3 L+a) \quad v^{\prime}=-\frac{q a b L}{2 E I} | |
| \delta_{B}=\frac{q}{24 E I}\left(3 L^{4}-4 a^{3} L+a^{4}\right) \quad \theta_{B}=\frac{q}{6 E I}\left(L^{3}-a^{3}\right) | |
 |
v=-\frac{P x^{2}}{6 E I}(3 L-x) \quad v^{\prime}=-\frac{P x}{2 E I}(2 L-x) |
| \delta_{B}=\frac{P L^{3}}{3 E I} \quad \theta_{B}=\frac{P L^{2}}{2 E I} | |
 |
v=-\frac{P x^{2}}{6 E I}(3 a-x) \quad v^{\prime}=-\frac{P x}{2 E I}(2 a-x) \quad(0 \leq x \leq a) |
| v=-\frac{P a^{2}}{6 E I}(3 x-a) \quad v^{\prime}=-\frac{P a^{2}}{2 E I} \quad(a \leq x \leq L) | |
| At x=a: \quad v=-\frac{P a^{3}}{3 E I} \quad v^{\prime}=-\frac{P a^{2}}{2 E I} | |
| \delta_{B}=\frac{P a^{2}}{6 E I}(3 L-a) \quad \theta_{B}=\frac{P a^{2}}{2 E I} | |
 |
v=-\frac{M_{0} x^{2}}{2 E I} \quad v^{\prime}=-\frac{M_{0} x}{E I} |
| \delta_{B}=\frac{M_{0} L^{2}}{2 E I} \quad \theta_{B}=\frac{M_{0} L}{E I} | |
 |
v=-\frac{M_{0} x^{2}}{2 E I} \quad v^{\prime}=-\frac{M_{0} x}{E I} \quad(0 \leq x \leq a) |
| v=-\frac{M_{0} a}{2 E I}(2 x-a) \quad v^{\prime}=-\frac{M_{0} a}{E I} \quad(a \leq x \leq L) | |
| At x=a: \quad v=-\frac{M_{0} a^{2}}{2 E I} \quad v^{\prime}=-\frac{M_{0} a}{E I} | |
| \delta_{B}=\frac{M_{0} a}{2 E I}(2 L-a) \quad \theta_{B}=\frac{M_{0} a}{E I} | |
 |
v=-\frac{q_{0} x^{2}}{120 L E I}\left(10 L^{3}-10 L^{2} x+5 L x^{2}-x^{3}\right) |
| v^{\prime}=-\frac{q_{0} x}{24 L E I}\left(4 L^{3}-6 L^{2} x+4 L x^{2}-x^{3}\right) | |
| \delta_{B}=\frac{q_{0} L^{4}}{30 E I} \quad \theta_{B}=\frac{q_{0} L^{3}}{24 E I} | |
 |
v=-\frac{q_{0} x^{2}}{120 L E I}\left(20 L^{3}-10 L^{2} x+x^{3}\right) |
| v^{\prime}=-\frac{q_{0} x}{24 L E I}\left(8 L^{3}-6 L^{2} x+x^{3}\right) | |
| \delta_{B}=\frac{11 q_{0} L^{4}}{120 E I} \quad \theta_{B}=\frac{q_{0} L^{3}}{8 E I} | |
 |
v=-\frac{q_{0} L}{3 \pi^{4} E I}\left(48 L^{3} \cos \frac{\pi x}{2 L}-48 L^{3}+3 \pi^{3} L x^{2}-\pi^{3} x^{3}\right) |
| v^{\prime}=-\frac{q_{0} L}{\pi^{3} E I}\left(2 \pi^{2} L x-\pi^{2} x^{2}-8L^{2} \sin \frac{\pi x}{2 L}\right) | |
| \delta_{B}=\frac{2 q_{0} L^{4}}{3 \pi^{4} E I}\left(\pi^{3}-24\right) \quad\theta_{B}=\frac{q_{0} L^{3}}{\pi^{3} E I}\left(\pi^{2}-8\right) | |